OSUstudent
- 10
- 0
Hello!
I have an application where I need to find the center of a circle where I am having trouble coming up with a simple way to do this. The diameter of the circle is known and i want to be able to determine the location of it where only a portion of the circle is known. (see the image below) I will know the location of a single point anywhere in the red circumference could anyone help me with this?
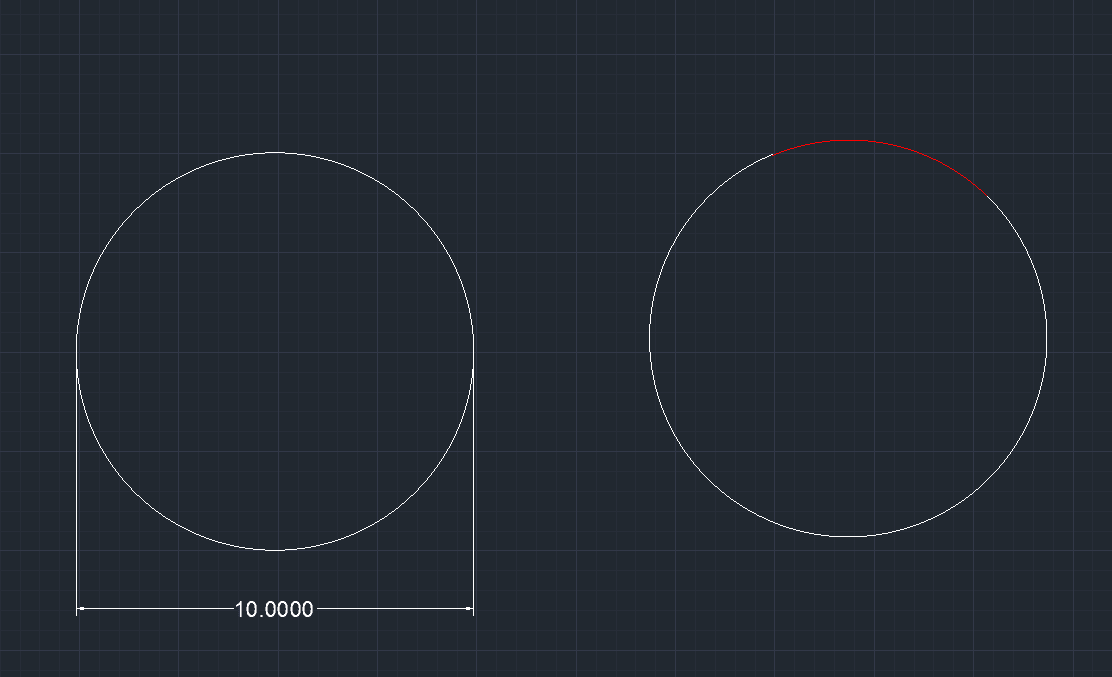
I have an application where I need to find the center of a circle where I am having trouble coming up with a simple way to do this. The diameter of the circle is known and i want to be able to determine the location of it where only a portion of the circle is known. (see the image below) I will know the location of a single point anywhere in the red circumference could anyone help me with this?