Finding the lengths and altitudes of s triangle

[paulmdrdo1]

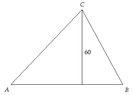
For a certain triangle ABC, sin A = 12/13, tan B = 15/8, and the altitude to side AB is 60 units. Find the lengths of the sides and of the altitudes of the triangle.

Again, I couldn't come up with an image of the triangle in question. Maybe you can provide me the picture of the problem so that I can solve it. Thanks!

 

[MarkFL]

Here is what I would begin with:

View attachment 3418

Now, if $$\sin(A)=\frac{12}{13}$$, then what must side $\overline{AC}$ be?

 

[paulmdrdo1]

Using $\csc(A)=\frac{AC}{60}$

$\frac{13}{12}=\frac{AC}{60}$

AC = 65 units

 

[MarkFL]

Using $\csc(A)=\frac{AC}{60}$

$\frac{13}{12}=\frac{AC}{60}$

AC = 65 units

Correct! :D

Now, can you use $$\tan(B)=\frac{15}{8}$$, along with what you already have to get $\overline{AB}$ and $\overline{BC}$, then use the area of the triangle to get the other two altitudes?

 

[paulmdrdo1]

yes I can do that.

Solving for $\overline{BC}$

$\csc(B)=\frac{\overline{BC}}{60}$

$\frac{17}{15}=\frac{\overline{BC}}{60}$

$\overline{BC}=68$units

for the length of line segment from point B to the intersection of the perpendicular line and $\overline{AB}$

$\sqrt{68^2-60^2}=32$

And for the length of line segment from point A to the intersection of the perpendicular line and $\overline{AB}$

$\sqrt{65^2-60^2}=25$

hence,

$\overline{AB}= 25+32=57$unitsI have no Idea where those two altitudes are.

 

[MarkFL]

yes I can do that.

Solving for $\overline{BC}$

$\csc(B)=\frac{\overline{BC}}{60}$

$\frac{17}{15}=\frac{\overline{BC}}{60}$

$\overline{BC}=68$units

for the length of line segment from point B to the intersection of the perpendicular line and $\overline{AB}$

$\sqrt{68^2-60^2}=32$

And for the length of line segment from point A to the intersection of the perpendicular line and $\overline{AB}$

$\sqrt{65^2-60^2}=25$

hence,

$\overline{AB}= 25+32=57$units

Yes, I agree with those side lengths. :D

Now, compute the area of the triangle, using $\overline{AB}$, and its given altitude, then use this area to find the altitudes relative to the other two sides. :D

 

[paulmdrdo1]

Hmm...

this is what I tried

$A=\frac{1}{2}{57}{60}=1710$ sq. units -->

from the result above solving for the altitude from point A to $\overline{BC}$

$1710=0.5(h)(68)$

$h=$50.29 units

solving for the altitude from point B to $\overline{AC}$

$1710=0.5(h)(65)$

$h=$ 52.6 units

Thank you very much! I couldn't have done this, if not for your help.

 

[MarkFL]

Yes, we can write:

$$h=\frac{2A}{b}=\frac{3420}{b}$$

So, relative to $\overline{AC}$, we have:

$$h=\frac{3420}{65}=\frac{684}{13}\approx52.6$$

And relative to $\overline{BC}$, we have:

$$h=\frac{3420}{68}=\frac{855}{17}\approx50.3$$