SUMMARY
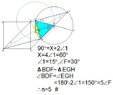
The discussion centers on determining the value of \( n \) in the context of a rhombus \( DBEF \) formed within square \( ABCD \). Given the conditions that \( CF \parallel BD \) and \( DF = DB \), it is established that \( \angle BDF = n \angle F \). The conclusion drawn is that \( n \) must equal 2, as the angles in a rhombus are equal and the geometric properties of the square dictate this relationship.
PREREQUISITES
- Understanding of geometric properties of squares and rhombuses
- Knowledge of parallel lines and their angle relationships
- Familiarity with angle measurement and relationships in polygons
- Basic algebra for solving equations involving angles
NEXT STEPS
- Study the properties of rhombuses and their angle relationships
- Explore geometric proofs involving squares and parallel lines
- Learn about angle bisectors and their applications in polygons
- Investigate the use of geometric constructions in solving angle problems
USEFUL FOR
Students of geometry, mathematics educators, and anyone interested in solving geometric problems involving polygons and their properties.