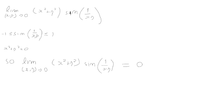Fixing Limits: Ensuring Correct Solutions with Proper Resolution Techniques
- Context: MHB
- Thread starter Fabio010
- Start date
-
- Tags
- Limits
Click For Summary
SUMMARY
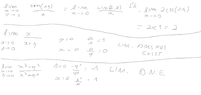
The discussion focuses on resolving limits in multivariable calculus, specifically using the squeeze theorem and the concept of path independence. The first limit discussed, \(\lim_{x,y\to 0} (x^2+y^2) \sin\left( \frac{1}{xy}\right)\), is confirmed to be zero. However, the second limit, \(\lim_{x \to 0}_{ y \to 2} \frac{\sin(xy)}{x}\), is incorrectly approached without proper justification for interchanging limits. The importance of using LaTeX for clarity in mathematical communication is also emphasized.
PREREQUISITES- Understanding of multivariable limits
- Familiarity with the squeeze theorem
- Basic knowledge of LaTeX for mathematical typesetting
- Concept of path independence in limits
- Study the application of the squeeze theorem in multivariable calculus
- Learn how to use LaTeX for clear mathematical presentations
- Research the implications of path independence in limits
- Explore the use of polar coordinates in evaluating limits
Students and educators in mathematics, particularly those focusing on calculus and limit evaluation techniques, as well as anyone looking to improve their mathematical communication skills using LaTeX.
Similar threads
- · Replies 9 ·
- · Replies 20 ·
- · Replies 3 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 4 ·
- · Replies 2 ·
- · Replies 8 ·
- · Replies 1 ·
- · Replies 3 ·