- #1
Yankel
- 395
- 0
Hello all,
I am trying to solve a limit:
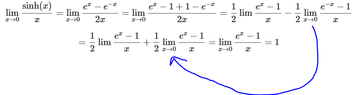
\[\lim_{x\rightarrow 0}\frac{sinh (x)}{x}\]
I found many suggestions online, from complex numbers to Taylor approximations.
Finally I found a reasonable solution, but one move there doesn't make sense to me.
I am attaching a picture:
View attachment 9401
I have marked in blue the move I can't understand. How does the minus from the exponent goes down before the half ?
And one more thing, at the final move, I know that the limit is 1, I know it as a rule, but why is this rule apply ? Thank you !
I am trying to solve a limit:
\[\lim_{x\rightarrow 0}\frac{sinh (x)}{x}\]
I found many suggestions online, from complex numbers to Taylor approximations.
Finally I found a reasonable solution, but one move there doesn't make sense to me.
I am attaching a picture:
View attachment 9401
I have marked in blue the move I can't understand. How does the minus from the exponent goes down before the half ?
And one more thing, at the final move, I know that the limit is 1, I know it as a rule, but why is this rule apply ? Thank you !