Forecasting metric using regression. Is this a sound approach?

[Wooody]

Hello,
First post here. I have some data I am trying to do some forecasting on and was hoping somebody who knows what they're actually doing can verify what I have done. A few years ago, the company I work for developed a mobile app for its customers and about 1 year ago they added some new features. The CTO came to me and asked me "Can you please give me a 12 month estimate on the number of customers using our mobile app?" and the data I have access to is:

(1) The number of customers registered each day for the last 8 years

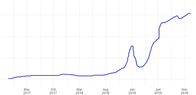
(2) The number of customers who used their customerId in the app for the last 2 yearsThe first thing I thought I should do is just use simple linear regression on (2) for the forecast. Here is a rough representation of what that data looks like:

View attachment 9308

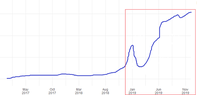
Firstly, if I was going to do a trend line here, would it be the right thing to do to just look at the data from around Jan of this year onwards where there is an obvious increase that aligns with the new features added to the app about a year ago (the red box below)?

View attachment 9309

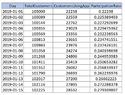
Then I thought about another way to do this which is to for each date, determine the total number of customers for each date (a rolling number) and the number of customers using their Id in the app on each date (rolling) so I could determine the number of customers using the app with their customerId as a percentage of total patients (called Participation Rate). A dummy dataset is as follows:

View attachment 9310

With this dataset I would do regression on the number of Total Customers and predict that in 12 months and do regression on the participation rate to predict that in 12 months and then simply multiply the two forecasted numbers together. Is this a sound approach? If not is there a better way to achieve this?

Thanks

 

[Jameson]

Hi Wooody,

Welcome to MHB! :)

What you have is a time-series. These problems are very common in business and have gotten a lot of attention lately in the world I work in - machine learning. The math of these problems can be tricky but I will say that you have a very good data source. 8 days of daily data is a great start to build a model.

Rolling averages are usually part of these types of models, so you have good intuition. For such an applied problem though there are many free software tools that might be useful. Have you ever used R or Python?? Are you more interested in the theory here or a workable solution?

 

[Wooody]

Hi Wooody,

Welcome to MHB! :)

What you have is a time-series. These problems are very common in business and have gotten a lot of attention lately in the world I work in - machine learning. The math of these problems can be tricky but I will say that you have a very good data source. 8 days of daily data is a great start to build a model.

Rolling averages are usually part of these types of models, so you have good intuition. For such an applied problem though there are many free software tools that might be useful. Have you ever used R or Python?? Are you more interested in the theory here or a workable solution?

Hi Jameson,
Thanks for your reply. I was a math major in college about 10 years ago but after I finished I went and worked in web development/business intelligence/database administration and haven't done any real math since, so I'm fairly rusty.

Yes, I am working with R at the moment.

I am interested in both the theory and getting a workable solution but if I had to pick, I'd choose the latter.

Would it be correct to use a ARIMA model?

 

[Jameson]

Hi Jameson,
Thanks for your reply. I was a math major in college about 10 years ago but after I finished I went and worked in web development/business intelligence/database administration and haven't done any real math since, so I'm fairly rusty.

Yes, I am working with R at the moment.

I am interested in both the theory and getting a workable solution but if I had to pick, I'd choose the latter.

Would it be correct to use a ARIMA model?

Hi Wooody,

Great info! Thank you. Time Series forecasting is something I'm working on quite a bit at my day job so this is a great problem for me to see. Unfortunately i work at a software company so our product is very expensive. What I would suggest is using ARIMA to start with and see how the forecasts work. You'll need to be comfortable breaking up the data into a few periods though to validate that it's working well. It would be something like this:

• Train on January through December
• Make predictions for next 1 year
• Check error of predictions and adjust
• Once final ARIMA model parameters are chosen, retrain model on most recent data

In your case you have a series that is significantly increasing over time, so doing something like differencing can help stabilize that jump to make better predictions.

Overall this is a tricky modeling problem and can take some time. If you are personally interested I think it's worth practicing because it's a great skill to develop. If you are under a time crunch then I think using a rolling average approach is a fine start. :)