How to - regression of noisy titration curve

[query_ious]

I'd appreciate advice on the correct statistical method to analyse a dataset -

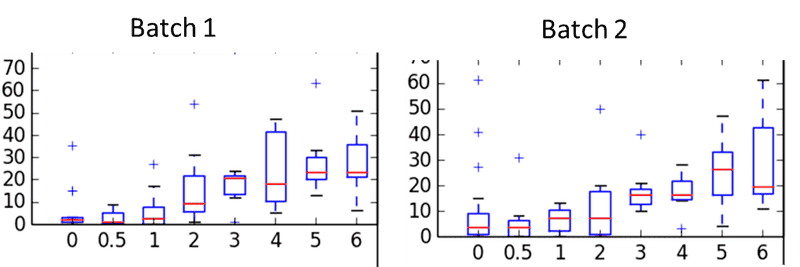
Dataset is basically a titration curve consisting of [0.5, 1, 2, 3, 4, 5, 6] pg of starting material and 8 replicates in each 'pg bin'. In 'stage 1' of the process each bin is labeled separately, in 'stage 2' all bins are pooled into one tube and amplified together and in 'stage 3' this is thrown into a DNA sequencer and bins are separated based on the labels.
So: the original input is a defined quantity of material and the final output is a number and what I would like to know is how accurately the output reflects the input. This feels like some kind of regression but I'm not sure what to use. The mean of 8 replicates? Their median? Something to do with the variability between them? Something based on a binomial sampling (with different bins having a different expected value?)?

Below is an example dataset - the x-axis is the titration curve bins ('0 pg' is background process noise), the y-axis is the 'output number' and the barplots are over the 8 replicates. There are 2 batches which are basically a repetition of the same experiment.

Thanks (and apologies if this has been asked before / is inappropriate)

<edit: uploading the image didn't work, I'm trying to fix this
for now - http://imgur.com/VRs5r6R

 

[SteamKing]

Your fix didn't take either.

 

[FactChecker]

Without knowing more details, I have one recommendation which is a general rule of thumb. Use the raw data without taking means or other processing. That will allow the statistical analysis to use the variation of the raw data within each category to determine the statistical strength of any results. I'm not sure that I understand your experiment, but it sounds like regression or analysis of variance techniques may apply.

 

[Doug Huffman]

On the face of it, without looking into the data and knowing just a little of colorimetry, regress both independent and dependent variables simultaneously.

 

[mfb]

I fixed the image.

I agree with FactChecker.
For the two batches, I would see if independent analyses of them give compatible results, and if yes, combine their datasets (so you get 16 repetitions per bin). If they are incompatible, you have to find out why.

 

[chiro]

What question are you trying to answer? Helping us understand this is a lot more useful than discussing statistical methodology as the choice of methodology is derived from the question, the data, and how to make use of both with statistical protocol and assumptions.

 

[query_ious]

Thanks for the replies.
I'll try to clarify the experiment:

1. From one original stock, set up 8 samples with different concentrations of RNA via dilution.
2. Take a fixed volume from each sample into one well of a 192 well plate such that each well contains between 0 to 6 pg of material. This means overall you have 24 'sampling replicates' for each original sample. (All pipetting done by a robot)
3. Split the plate into 3 batches, do more molecular biology, throw into a DNA sequencer.
*Note - the RNA is a mix of many different genes and the molecular biology extracts data for multiple genes in parallel. The observed value is essentially a count of how many molecules were in the original sample, so for each well there are actually 8 datapoints, each one reflecting the estimated count for a different gene (with a different original count).

There are 2 goals for the dataset -
1) How different are different experimental batches? E.g. how much noise does the molecular biology + sequencing introduce?
2) Within a single batch, how accurately does the observed value reflect the initial value? So if I observe a value of '10' for some datapoint, what is my distribution over likely initial values? (Or at minimum - what information does an x-fold difference in observed values of two samples give me about the fold difference in initial values of 2 samples?)

I've asked around campus and the recommendation has been to start by looking at things like variance vs. mean plots, playing around with generative simulations, and
binning different batches and/or different genes to assess the type of model to use. After that look at the slope of the titration and maybe more fancy stuff. I also might do another experiment or two over a larger range with more replicates for more power.

Are there any specific things you would watch out for? Any rules of thumb for how much statistics are necessary to answer the above 2 questions?
I suppose it might be a bit overambitious given that I'm kind of asking for magical solutions over an internet conversation but I'd still appreciate any input :)

Below is another example image (for two genes). x-axis is the theoretical RNA input (with a small x-staggering to separate dots), y-axis is the molecule count. regression is mostly as a visual aid at this point...

<@mfb thanks for fixing my earlier image, I just copy-pasted your webscript to upload this one though I have to say I have no clue why it works>

 

[chiro]

Usually when people look at differences they do it to the mean or median or some other similar value. Doing this across multiple datasets is called an ANOVA in statistical lingo and there are many types of ANOVA depending on the assumptions of your distribution and your data.

If you are looking at noise then you need a model for said noise. There are models but they can be complicated depending on how equally complicated your process is.

The things that contribute to this are the decomposition of the residual itself along with any sort of covariance structure that may exist between observations and/or between the noise terms. This can actually get involved to the point where graduate statistics theory and knowledge is involved. If this is the case then you should really speak to a statistician or perhaps a PhD student or a TA or someone like that.

Models between random variables in terms of mean responses are called regression models. You need to specify the structure of the model before you pick the regression analysis methods (and execute them) but once you do you can get the results (usually done via statistical software like SAS or R) and use that to help form conclusions. The output needs to be understood not only in terms of the values but what assumptions you use to generate said results. If they don't work well and don't match up then your conclusions will be invalid and someone will likely pick it up. It helps to spend a little time on getting this stuff right. Regressions can help you model relations between two variables including linear and non-linear models in various ways. Any book on regression modeling will go through both theory and practice. If you are in a university your computers will probably have SAS which is what I recommend - especially if you've never done any programming before.

For the second point you need to determine whether data points are independent or not. If they are independent then one never determines the other. If they are dependent then you need to look at the joint distribution and use a statistical test to see whether your hypothesis holds. Again this involves making assumptions and understanding biology so that this understanding can be used to get statistical assumptions to come up with a model and to test hypotheses.

Usually what happens in statistics is that you measure a parameter which is tied to some distribution assumptions. A sample contains information that is used to estimate said parameter and the higher the information content in the sample, the better the estimate is. If you are figuring out means then you use the central limit theorem when the sample size is large enough (basically any time you use an expectation in some way). Independent data points increase information and you can use this idea to figure out how much data you need to get a good enough interval for estimating your parameter.

I know this is a lot to take in but it will help you down the road. Making mistakes will screw up your analysis and if you publish a paper using said results and they are wrong then you will wasted some time - which is why I recommend you speak to a statistician, PhD student, TA, or RA in addition to finding out about ANOVA and Regression Models.

If you have other specific questions I can do my best to answer them.

 

[Stephen Tashi]

1. From one original stock, set up 8 samples with different concentrations of RNA via dilution.
2. Take a fixed volume from each sample into one well of a 192 well plate such that each well contains between 0 to 6 pg of material. This means overall you have 24 'sampling replicates' for each original sample. (All pipetting done by a robot)

Lets say step 1 produces 8 "bottles" B{1},B[2],...B[8] of different concentrations of RNA. Is there anything systematic about how the concentrations are prepared? Or are they just "different" ?

For each bottle B[k} , the 192 well plate has 24 wells filled with solution from bottle B[k].
Are there any wells actually filled with 0 pg of bottle B[k] solution? Or are there 4 wells for each amount 1,2,3,4,5,6 pg ?

3. Split the plate into 3 batches, do more molecular biology, throw into a DNA sequencer.

What is in a batch? If each batch contains 8 wells filled with solution from bottle B[k]. I don't understand how the 4 wells with (say) 2 pg of solution would be divided into 3 batches? Or do you divide them into 4 batches and use one batch as an experimental "control"?

From what you say below, a different treatment is give to each batch (i.e. You aren't trying to give each batch the same treatment.).

*Note - the RNA is a mix of many different genes and the molecular biology extracts data for multiple genes in parallel. The observed value is essentially a count of how many molecules were in the original sample, so for each well there are actually 8 datapoints, each one reflecting the estimated count for a different gene (with a different original count).

What is theoretical effect of the treatment on a well? If you are counting particles of type W, does it multiply the particles of W that were originally present in each well by some constant number?

There are 2 goals for the dataset -
1) How different are different experimental batches? E.g. how much noise does the molecular biology + sequencing introduce?
2) Within a single batch, how accurately does the observed value reflect the initial value? So if I observe a value of '10' for some datapoint, what is my distribution over likely initial values? (Or at minimum - what information does an x-fold difference in observed values of two samples give me about the fold difference in initial values of 2 samples?)

Compared to statements of goals we see in other threads, that's remarkably clear.