Discussion Overview
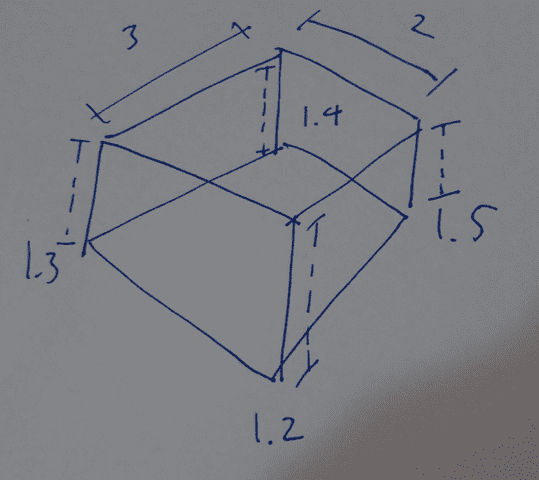
The discussion revolves around finding a formula to calculate the volume of a solid with a fixed width and depth but varying heights at its corners. Participants explore different mathematical approaches, including integration and geometric considerations, to address this problem.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants suggest that the volume calculation depends on the shape of the top face, which is not necessarily planar.
- One participant proposes using integration to find the volume, suggesting to define the top face with an equation of the form z = f(x,y) and calculate the integral over the defined area.
- Another participant emphasizes the importance of knowing the function describing the top face, as it significantly affects the volume calculation.
- Some participants discuss the possibility of fitting a plane to the coordinates of the top face to estimate the volume, while acknowledging that this may not accurately reflect the true shape.
- There are differing views on whether the top face can be treated as a plane, with some asserting that the vertical sides must meet specific conditions for this to hold true.
- Participants express uncertainty about how to derive the equation of the plane representing the top face and discuss methods such as using vectors and cross products.
Areas of Agreement / Disagreement
Participants generally do not reach a consensus on a specific formula or method for calculating the volume. Multiple competing views and approaches remain, with ongoing discussions about the implications of the top face's shape.
Contextual Notes
Limitations include the assumption that the top face can be approximated as a plane, which may not hold true in all cases. The discussion also highlights the need for additional information about the interior of the solid to improve volume estimation.