Buzz Bloom
Gold Member
- 2,517
- 465
- TL;DR
- I need help to figure out how the formula for the velocity of a circular orbit can be derived from the Schwartzschild metric .
Below are equations/formulas/text from
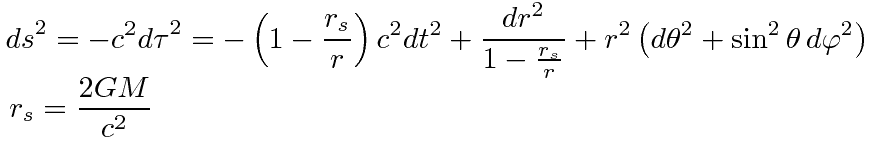

I apologize for not remembering the source for the "v=" equation, or for my inability to find it again.
For a circular orbit, the distance r and proper distance s are both constant. Therefore
##{r^2 {dθ}^2} = {c^2} /sqrt {1-r_s/r}} {dt}^2 ##
## r = 1##
I apologize for not remembering the source for the "v=" equation, or for my inability to find it again.
For a circular orbit, the distance r and proper distance s are both constant. Therefore
ds = dr = 0.
Assume the coordinates are such that the orbit has:sin ϑ = 1, and dϑ = 0.
Therefore the metric an be written##{r^2 {dθ}^2} = {c^2} /sqrt {1-r_s/r}} {dt}^2 ##
## r = 1##