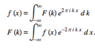The discussion centers on the application of the Fourier transform to calculate the power of a signal. It clarifies that the function f(x) in the context of Fourier transforms represents the original signal x(t), not its power. The Fourier transform, denoted as X(f) or X_n, is utilized to analyze the frequency components of the signal, and it is essential to take the absolute value of the result after performing the Fourier transform to obtain meaningful power information.
PREREQUISITESElectrical engineers, signal processing students, and anyone involved in analyzing power signals using Fourier transforms will benefit from this discussion.
