Frequency to temporal period conversion

[roam]

I am working with signals that look like the following. The curve has the same form in both frequency and time domain.

I am trying to calculate the ratio of two distances:
The distance between two adjacent red "x"s (known as the free spectral range (FSR)).
The distance between two adjacent green "x"s (FWHM of the dips).

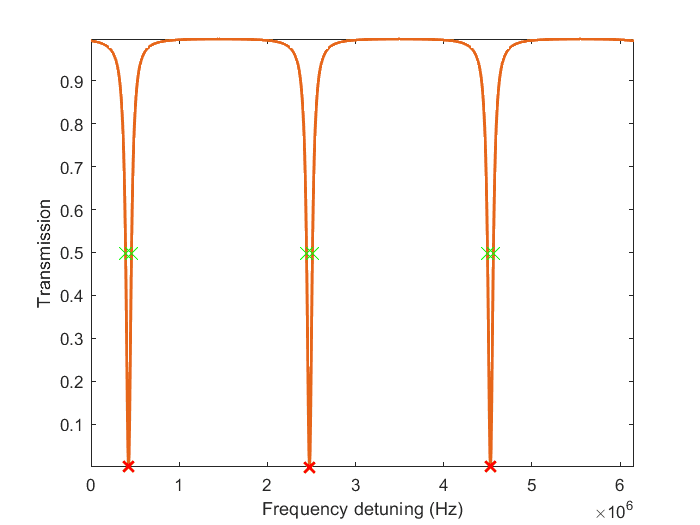
For the simulation above I get $\text{FSR} = 2.05 \times 10^6 Hz$, and $\text{FWHM} = 6.6 \times 10^4 Hz$. So a calculation in frequency domain gives the correct answer:

$$2.05 \times 10^6 / 6.6 \times 10^4 = 30.6,$$

whereas with conversion to time domain I get:

$$(1/2.05 \times 10^6) / (1/ 6.6 \times 10^4) = 0.0326.$$

Note that FWHM of a curve must be smaller than FSR in both time and frequency domain. But when I take the inverse of these values (i.e., shift to time domain), FWHM appears to be larger than FSR!

Here is an actual time domain measurement. As one can see, it has the same general shape as it would in the frequency domain:

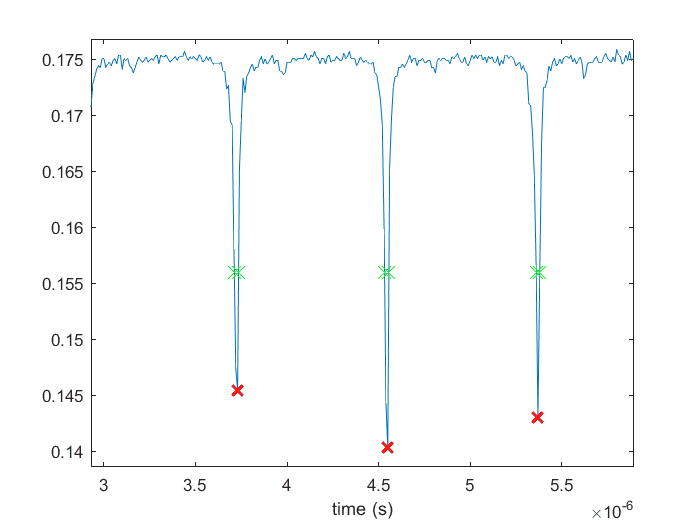
Again, if I calculate the ratio in time domain I get the right answer, but conversion to frequency domain does not give the right answer. Why is that?

Any explanation would be appreciated.

 

[Dale]

1/30.6=0.0326

Note that FWHM of a curve must be smaller than FSR in both time and frequency domain.

That is sort of true. If you were considering a single domain then yes. But the FWHM in the frequency domain corresponds to something with a long time in the time domain, and he FSR in the frequency domain corresponds to something with a very small time in the time domain.

So the thing that corresponds to the FSR in one domain corresponds to the FWHM in the other domain. That is why you need to invert your calculation in the time domain