dynamicskillingme
- 26
- 0
Homework Statement
For a gauge function G(t,q) where
does
The discussion focuses on the gauge function G(t,q) in the context of Lagrangian mechanics and its derivatives. Participants clarify the relationship between G and its variables, emphasizing the expression of the time derivative of G as 𝜎G = \frac{\partial G}{\partial q} \dot{q} + \frac{\partial G}{\partial t}. The ability to interchange the order of derivatives is confirmed under the condition that G is a function of both q and t. The conversation highlights the importance of understanding the Euler-Lagrange equations and generalized momenta in mechanical systems.
Students and researchers in physics, particularly those focusing on classical mechanics, Lagrangian dynamics, and mathematical physics. This discussion is beneficial for anyone looking to deepen their understanding of gauge transformations and their applications in mechanical systems.
stevendaryl said:Oh, so you're just talking about Lagrangian mechanics.
If G is a function of q and t, then you have:
\dot{G} = \frac{\partial G}{\partial q} \dot{q} + \frac{\partial G}{\partial t}
So in that case, \frac{\partial \dot{G}}{\partial \dot{q}} = \frac{\partial G}{\partial q}
dynamicskillingme said:A quick question about the same function, wouldbe a true statement?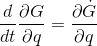
stevendaryl said:Yes, if G is only a function of q and t.
dynamicskillingme said:G is a function of q and t, (G(t,q) to be exact). Could you explain why you can change the order of the derivatives in this case?