Gear Ratios and Constant Power/Torque: find max velocity?

[jzmaster]

I'm trying to determine how exactly gear ratio limits velocity. I know that a high torque configuration is generally regarded as low speed, but my calculations do not seem to support that.

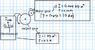
Basically, I've written a small problem where we have an input gear with constant torque and an output gear with a load on it. If I apply a gear ratio of 1, I get a lower angular acceleration than if I do a gear ratio of 10 (output has 10 times the teeth) -- this makes sense.

When calculating maximum angular velocity though (assuming about 0.3*<omega> on the output gear), I get a maximum velocity that is much larger than with a lower gear ratio. The torque is the same, the power required is very large (orders of magnitude difference). I am assuming 100% transmission efficiency.

So, if we have a motor which can produce constant torque regardless of RPM (possibly in excess of 22000) while being able to provide the necessary power, is it reasonable to say that the output gear would be driven at a faster speed than if the gear ratio was 1? Attached is a quick sketch of my problem.

 

[Baluncore]

Rate of energy flow = Power = Torque * RPM.

 

[JBA]

Simply put, the speed ratio of the output gear to the motor gear is the inverse of the output gear diameter / motor gear diameter, i.e for a 1/3 gear ratio the output gear rpm will 3 times the motor rpm. This speed ratio totally independent of the motor power or the output gear loading.

 

[Randy Beikmann]

If you assume constant motor torque regardless of its speed, you are essentially allowing it to produce limitless power as its speed increases. Your best acceleration is with an extremely high amount of gear reduction, and the torque multiplication that comes with it. But your motor speed would be extremely high, and since power = torque times angular velocity, your power would have to be huge.
In real motors, torque will drop with higher speed, batteries are limited in how much power they can supply, and air flow restriction into an engine limits its power.