General natural boundary condition?

[maistral]

TL;DR

A little clarification with regard to the natural boundary condition.

Hi, I'd like to be clarified regarding the general natural/Neumann boundary condition for a PDE.

1. The natural boundary condition is generally defined as:

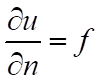(1)
and can be expressed as, according to this resource:

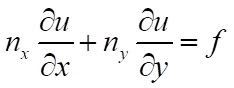(2)

But apparently, according to https://www.researchgate.net/post/How_to_impose_natural_boundary_conditions_with_Generalized_Finite_Difference_Method_or_meshfree_collocation_method resource (posted by Dr. Fan):

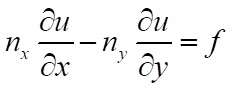(3)

Which is which? Is it supposed to be positive, or negative? When should it be positive or negative?

2. If I apply the derivative boundary condition, on say, the bottom of a square plate, I can state:

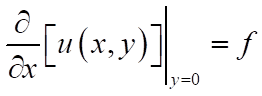(4)
or for simplicity,

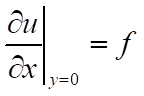(5)

Obviously, comparing it with (2), n_y is equal to 0. Why is this so? Why is n_y = 0?

Thanks!

 

[Orodruin]

1. The minus sign is an obvious typo.
2. $\vec n$ is the normal vector. The normal vector's y-component on a coordinate surface of $y$ is zero.

 

[maistral]

Hi! Thanks for replying. Thank you very much, it did clarify a lot of things. I still have two remaining problems, however.

1. Where is the vector n exactly pointed to? Is it going towards the region, or is it going away from the region?

2. I am assuming that the complete form of the Neumann condition is used for irregular boundaries (ie. curved ones, so on and forth). As stated by the first resource, n_x = cos θ, and n_y = sin θ.

If I use finite element analysis, I can just take the normal vector perpendicular to the edge of the element which is definitely a no-brainer as it's a straight line.

My problem begins to appear if I begin using finite differences. How do I exactly implement this kind of boundary condition on nodes? I'm confused - nodes are, well, nodes; just a point. I'm under the impression that I can get the angle required for calculating n_x and n_y by taking the tangent of the irregular boundary curve at the node, then I draw the perpendicular line needed to calculate the angle. Is this even correct?