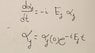Discussion Overview
The discussion revolves around the Generalized Schrödinger equation as presented in a lecture by Prof. Susskind. Participants are examining the treatment of time dependence in the coefficients of eigenvectors of a wave function, particularly focusing on the role of the exponential term e^(-iEt).
Discussion Character
- Technical explanation, Conceptual clarification, Debate/contested
Main Points Raised
- One participant questions why the exponential term e^(-iEt) is not explicitly included in the top equation of the attachment, suggesting it may be disregarded as just a number.
- Another participant asserts that the exponential is present but represented as 'alpha' on the right-hand side of the equation.
- A different participant seeks clarification on whether the conflation of \alphaj(0)e^(-iEt) into \alphaj is valid, given that e^(-iEt) is not a constant.
- It is noted that the only variable in the context is time, with e^(-iEt) encapsulating the time dependence of alpha.
- One participant reiterates the question about the conflation of terms, emphasizing that Aj is defined in the attachment and does not appear to be a constant.
Areas of Agreement / Disagreement
Participants express differing views on the treatment of the exponential term and its representation in the equation. The discussion remains unresolved as to whether the conflation of terms is appropriate.
Contextual Notes
There are limitations regarding the clarity of the attachment and the definitions of terms used in the discussion, which may affect the understanding of the arguments presented.