Generating/spanning modules and submodules .... ....

[Math Amateur]

In Chapter 1 of his book: "Modules and Rings", John Dauns (on page 7) considers a subset $T$ of an R-module $M$ and defines the R-submodule generated by $T$ ... for which he uses the notation $\langle T \rangle$ ... ... as follows:

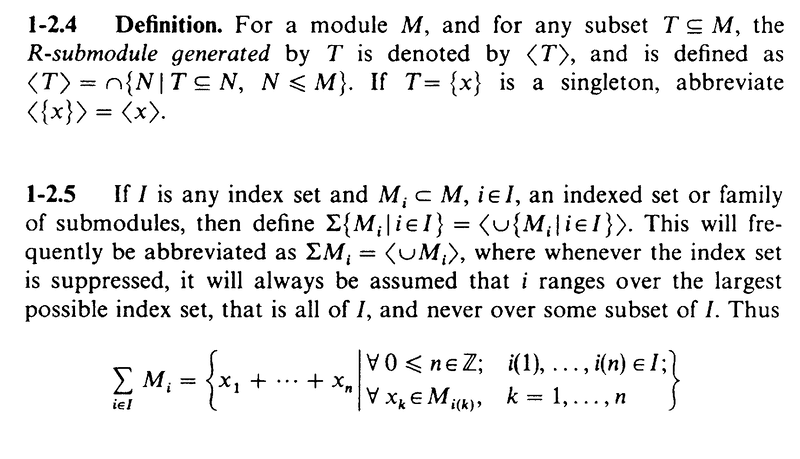
Now, note that Dauns (in Section 1-2.5) also defines $\sum M_i = \langle \cup M_i \rangle$ ... and so it follows (I think) that if the family of submodules, $\{ M_i \}_I$ spans or generates $M$ ... then we have

$\{ M_i \}_I$ generates/spans $M \Longrightarrow M = \sum M_i = \langle \cup M_i \rangle$ ... ... ... ... ... (1)Note that on page 8, under the heading Observations, Dauns states:

" ... ... if $1 \in R, \langle T \rangle = \sum \{ tR \mid t \in T \}$ ... ... ... ... ... (2)Now, we have that

(1) (2) $\Longrightarrow M = \sum M_i = \langle \cup M_i \rangle = \sum \{ tR \mid t \in \cup M_i \}$ ... ... ... ... ... (3)But ... how do we reconcile Dauns' definitions with Bland's Definition 4.1.2 which states

" ... ... An R-module M is said to be generated by a set $\{ M_\alpha \}_\Delta$ of R-modules if there is an epimorphism $\bigoplus_\Delta M_\alpha \to M$. ... ... "The complete Definition 4.1.2 by Bland reads as follows:

Can someone please explain how to reconcile Dauns' and Bland's definitions ...Just a note ... I feel that Dauns definition has more the "feel" of something being generated ...
To give readers of the above post the context including the notation of Dauns approach I am providing the text of Sections 1-2.4 to 1-2.8 ... as follows ...

 

[fresh_42]

The only essential difference between the two definitions is, that Bland uses a sum of any modules $M_\alpha$, which are external to $M$, and Dauns starts with elements, which are already in $M$. So we should first make them comparable. Let's take Bland's notation and write
$$
\bigoplus_{\alpha \in \Delta}M_\alpha = \{\,(m_\alpha)_{\alpha\in \Delta}\,|\,m_\alpha \in M_\alpha\,\}\text{ and } \iota_\alpha\, : \,M_\alpha \longrightarrow \bigoplus_{\alpha \in \Delta}M_\alpha\, , \,\iota(m_\alpha)=(0,\ldots,m_\alpha,\ldots,0,\ldots)
$$
We get Dauns' definition now by setting $T:=\cup \iota_\alpha(M_\alpha)\subseteq M$. And in the other direction, if we already have $M=\sum_\alpha M_\alpha$ then the projection is clear.

 

[Math Amateur]

The only essential difference between the two definitions is, that Bland uses a sum of any modules $M_\alpha$, which are external to $M$, and Dauns starts with elements, which are already in $M$. So we should first make them comparable. Let's take Bland's notation and write
$$
\bigoplus_{\alpha \in \Delta}M_\alpha = \{\,(m_\alpha)_{\alpha\in \Delta}\,|\,m_\alpha \in M_\alpha\,\}\text{ and } \iota_\alpha\, : \,M_\alpha \longrightarrow \bigoplus_{\alpha \in \Delta}M_\alpha\, , \,\iota(m_\alpha)=(0,\ldots,m_\alpha,\ldots,0,\ldots)
$$
We get Dauns' definition now by setting $T:=\cup \iota_\alpha(M_\alpha)\subseteq M$. And in the other direction, if we already have $M=\sum_\alpha M_\alpha$ then the projection is clear.

Thanks fresh_42 ...

Still reflecting on your post ...

Peter

 

[steenis]

The definitions of Bland and Dauns are the same, compare definition 1.4.3. of Bland with definition 1-2.4 of Dauns. Use proposition 1.4.4. of Bland and 1-2.5 of Dauns to see that the definitions are the same. So let’s concentrate on Bland.
You could first read post #2 of
https://mathhelpboards.com/linear-abstract-algebra-14/modules-generated-sets-submodules-bland-problem-1-problem-set-4-1-a-24243.html

(Recall: If $(M_\alpha)_\Delta$ is a family of R-modules such that $M_\alpha = M$ for each $\alpha \in \Delta$ then $\Pi_\Delta M_\alpha$ and $\bigoplus_\Delta M_\alpha$ will be denoted by $M^\Delta$ and $M^{(\Delta)}$, respectively).

Generated vs. spanned.
(def.1.4.3.p29) Let $S \subset M$, $M$ is generated by (the elements of) $S$ if each element $x \in M$ can be expressed as a finite sum $x = \Sigma x_\alpha a_\alpha$ with $x_\alpha \in S$ and $a_\alpha \in R$.

(p.104) Let $\mathscr{S} = \{N_\alpha\}_\Delta$ be a set of submodules of M such that $M = \Sigma_\Delta N_\alpha = \{\text{ finite sums } \Sigma x_\alpha a_\alpha \text{ with } x_\alpha \in N_\alpha \text{ and } a_\alpha \in R \}$ then $\mathscr{S}$ is said to span $M$. $\mathscr{S}$ is called the spanning set.

Thus $M$ is generated by elements of $M$, and $M$ is spanned by submodules of $M$.

(p.28, p.51) Clear is that if $M$ is generated by $\{x_1, \cdots, x_n\}$ then $M$ is spanned by the submodules $\{x_1R, \cdots, x_nR \}$, and conversely:

$M = \langle x_1, \cdots, x_n \rangle$ $\Longleftrightarrow$ $M = \Sigma x_i R$.

You can prove that yourself. This is also valid for infinite sets of generators and spanning sets.

For instance $\mathbb{R}^3$ is spanned by $x\mathbb{R}$, $y\mathbb{R}$, and $z\mathbb{R}$, the x-axis, y-axis, and z-axis, respectively.
If $x \in M$ then $x\mathbb{R}$ is a submodule of $M$, and it is a very special submodule of $M$. You can wonder if $M$ can be spanned by more general submodules of $M$ ?. Can $M$ be generated by modules that are outside of $M$, i.e., that are not submodules of $M$ ?. For instance, can the real plane $\mathbb{R}^2$ be spanned by a sphere or a torus? To answer these questions, Bland introduced a “new” definition of generating a module.

Bland Definition 4.1.2.
(1) An $R$-module $M$ is said to be generated by a set $(M_\alpha)_\Delta$ of R-modules (or $(M_\alpha)_\Delta$ generates $M$) if there is an epimorphism $\bigoplus_\Delta M_\alpha \to M$.

(2) An $R$-module $M$ is said to generate an $R$-module $N$ if there is an epimorphism $M^{(\Delta)} \to N$ for some set $\Delta$.

Annoying is that Bland (and all other authors) now speak of generating a module with (other) modules instead of spanning a module with modules. We have to live with this confusing mix of terms.

Let us now go back to free modules and recall this important theorem:
Bland Proposition 2.2.6.p.54
Every $R$-module $M$ is the homomorphic image of a free $R$-module. Furthermore, if $M$ is finitely generated, then the free module can be chosen to be finitely generated.
Recall that every module $M$ has at least one set of generators, namely $M$ itself.
What does this theorem say? It says (you can check it in your textbook):
For each module $M$ there exists an index set $\Delta$ $\text{ AND }$ an epimorpism $F:R^{(\Delta)} \to M$.

That’s it. The set $\Delta$ may be finite or infinite.

Now compare this with part (2) of definition.4.1.2. above.

I think this reconciles this new definition with the former definitions of Bland.

Of course part (1) of definition 4.1.2 is a generalization of part (2).

 

[fresh_42]

Thus $M$ is generated by elements of $M$, and $M$ is spanned by submodules of $M$.

This is a bit too artificial for my taste. There is not really a clear definition for either of them, except that generate extends to non-linear structures as groups and spanned usually refers to linear structures as modules and vector spaces. They are often used equivalently, so what looks like a definition above is by no means general and might even be inconsistent within Bland's book. Whether a module is generated by something or spanned by something doesn't matter.

So the terms might only apply to: (see next post)

 

[steenis]

It is not my definition, there are definitions of Bland.

In def.1.4.3 Bland defines generated by elements
On p.104 Bland defines spanned by submodules
In def.4.1.2 Bland defines generated by modules
Mathamateur is struggling with these notions and asked for “reconciliation”