Discussion Overview
The discussion revolves around a geometry problem involving a square and trapeziums, where participants are tasked with expressing a length in terms of a variable and finding its numerical value. The scope includes mathematical reasoning and problem-solving related to geometry and algebra.
Discussion Character
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
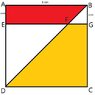
- One participant introduces the problem and requests help with expressing the length of FG in terms of x and finding the value of x.
- Another participant suggests using the area formula for trapeziums to derive an equation involving FG and x.
- Multiple participants confirm the correctness of the derived equation for FG and express it in terms of x as $$\overline{FG}=\frac{5x-1}{1+x}$$.
- There is a discussion about the similarity of triangles BFG and BDC, leading to the conclusion that $$\overline{FG}=x$$ under certain assumptions.
- One participant questions the assumption that BFD is a straight line, suggesting it may affect the deduction process.
- Another participant states that without assuming BD is a diagonal, finding the value of x may not be possible.
- Several participants report finding the numerical value of x, with one stating it as approximately 0.27.
Areas of Agreement / Disagreement
Participants express differing views on the assumptions necessary for solving the problem, particularly regarding the straightness of line BFD. While some agree on the derived equations, the discussion remains unresolved regarding the implications of these assumptions on the final answer.
Contextual Notes
There are unresolved assumptions about the geometric configuration, particularly concerning the straightness of line BFD and its impact on the calculations. The discussion includes multiple derived expressions for FG and varying interpretations of the problem's conditions.