SUMMARY
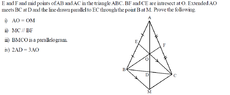
The discussion focuses on the midpoint theorem in geometry, specifically regarding triangle properties and congruence. The key theorem states that if a line passes through the midpoint of one side of a triangle and is parallel to another side, it will also pass through the midpoint of the third side. Participants confirm that triangles ODC and MBA are congruent, leading to the conclusion that BMCO forms a parallelogram. The proof involves using congruence and properties of parallelograms to establish relationships between segments and midpoints.
PREREQUISITES
- Understanding of triangle congruence criteria, specifically SAA (Side-Angle-Angle).
- Familiarity with the properties of parallelograms.
- Knowledge of the midpoint theorem in geometry.
- Basic skills in geometric proofs and reasoning.
NEXT STEPS
- Study the properties of triangle congruence, focusing on SAA and its applications.
- Learn more about the midpoint theorem and its proofs in various geometric contexts.
- Explore the characteristics and properties of parallelograms in geometry.
- Practice solving geometric proofs involving midpoints and parallel lines.
USEFUL FOR
Students studying geometry, educators teaching geometric concepts, and anyone interested in mastering geometric proofs and theorems related to triangles and parallelograms.