bnich
- 1
- 0
- TL;DR
- Getting zero's and poles for Laplace transform of damped cosine
I'm following the intuition behind getting the zero's and poles of a damped cosine function with this video
At around 11:50, he shows some graphics pertaining to multiplying the probing function with the impulse response, but the graphics don't seem correct.
For example, in the B+B' graphic, the probing function exactly equals the impulse response, but should the probing function be the inverse of the impulse response in order for the sum to be "just barely infinite" as depicted in the screenshot
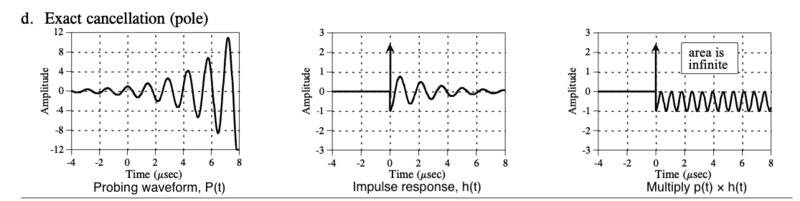
Image source: http://www.dspguide.com/CH32.PDF
And for the D graphic, the complex part should be zero, but shouldn't the real part of the exponential be the same as where the poles are? Image below describes what I think it should be
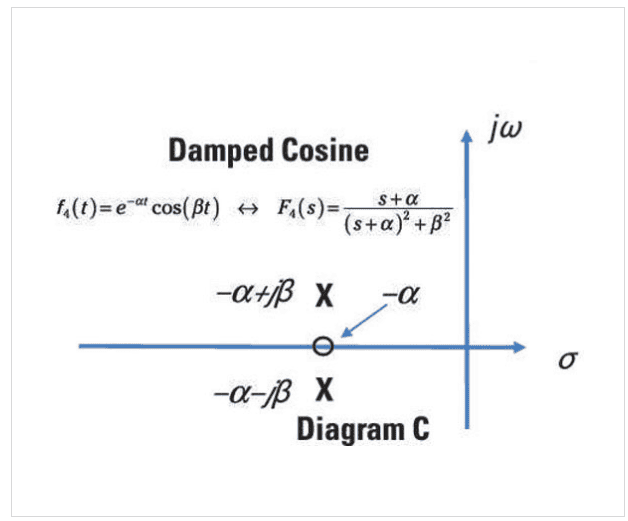
image source: https://www.dummies.com/article/tec...s-understanding-poles-and-zeros-of-fs-166275/
Thanks for your time. I look forward to hearing some feedback!
At around 11:50, he shows some graphics pertaining to multiplying the probing function with the impulse response, but the graphics don't seem correct.
For example, in the B+B' graphic, the probing function exactly equals the impulse response, but should the probing function be the inverse of the impulse response in order for the sum to be "just barely infinite" as depicted in the screenshot
Image source: http://www.dspguide.com/CH32.PDF
And for the D graphic, the complex part should be zero, but shouldn't the real part of the exponential be the same as where the poles are? Image below describes what I think it should be
image source: https://www.dummies.com/article/tec...s-understanding-poles-and-zeros-of-fs-166275/
Thanks for your time. I look forward to hearing some feedback!