Discussion Overview
The discussion revolves around the equation x - |x| = y - |y| and the process of graphing it. Participants explore how to break down the equation into different cases based on the signs of x and y, and the implications for the graph in various quadrants.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant proposes breaking down the equation into four cases based on the signs of x and y, leading to different equations for each quadrant.
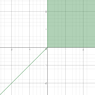
- Another participant suggests that the first equation is valid in the first quadrant, indicating that all points in this quadrant belong to the graph.
- Further clarification is provided regarding the conditions for each case, noting that the second and third equations only include boundary points with the first quadrant, while the fourth equation indicates that the line y = x is part of the graph in the third quadrant.
- A later reply expresses surprise at the conclusion that an entire quadrant is included in the graph, indicating a lack of prior awareness of this concept.
Areas of Agreement / Disagreement
Participants generally agree on the breakdown of the equation into cases and the implications for the graph, but there is some uncertainty regarding the completeness of the initial approach and the conditions under which each case applies.
Contextual Notes
Some assumptions about the conditions for x and y are discussed, but there may be limitations in fully resolving the implications of the equations across all quadrants.
Who May Find This Useful
Individuals interested in graphing piecewise functions, understanding absolute value equations, or exploring mathematical reasoning in different quadrants may find this discussion beneficial.