Gravitational Potential energy problem

[aero_zeppelin]

Homework Statement

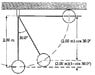
A 400-N child is in a swing that is attached to ropes 2.00 m long. Find the gravitational potential energy of the child–Earth system relative to the child’s lowest position when (a) the ropes are horizontal, (b) the ropes make a 30.0° angle with the vertical, and (c) the child is at the bottom of the circular arc.

Homework Equations

Ug = mgy

The Attempt at a Solution

For a) there was no problem.

For b) I thought it was as simple as applying Ug = mgy cos 30° = (400 N)(2.0 m) cos 30°

But the book says its Ug = mgy (1-cos 30°)

That's my confusion... why 1 - cos 30° and not cos 30° by itself??

any help? Thanks in advance!

 

[PhanthomJay]

The problem is asking for the GPE relative to the lowest position. For part (b), the figure shows that 2 cos 30 is the vertical distance from the swing to its ropes attachment point. You want the vertical distance from the swing to the low point.

 

[aero_zeppelin]

The problem is asking for the GPE relative to the lowest position. For part (b), the figure shows that 2 cos 30 is the vertical distance from the swing to its ropes attachment point. You want the vertical distance from the swing to the low point.

Ok but why substract 1 - cos 30°? :(

thanks for the help!

 

[PhanthomJay]

In the 30 degree position, the vert distance from the swing to the top is 2cos30 m. The vert distance from the low point of the swing to the top is 2. Thus, the distance from the swing in its 30 degree position to the low point is (2) - (2cos30) = 2(1-cos30) m.

 

[aero_zeppelin]

lolll it's only factored out right??

Thanks a lot!