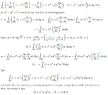Green's theorem - Boundary value problem has at most one solution

[mathmari]

Hey!

Prove using Green's theorem that the boundary value problem $$\frac{\partial}{\partial{x}}\left ( (1+x^2)\frac{\partial{u}}{\partial{x}}\right )+\frac{\partial}{\partial{y}}\left ( (1+x^2+y^2)\frac{\partial{u}}{\partial{y}}\right ) -(1+x^2+y^4)u=f(x,y), x^2+y^2<1 \\ u(x, y)=g(x,y), x^2+y^2=1$$ has at most one solution.

I have done the following:

We suppose that the problem has two different solutions $u_1, u_2$. Then $w=u_1-u_2$ solves the problem:

$$\frac{\partial}{\partial{x}}\left ( (1+x^2)\frac{\partial{w}}{\partial{x}}\right )+\frac{\partial}{\partial{y}}\left ( (1+x^2+y^2)\frac{\partial{w}}{\partial{y}}\right ) -(1+x^2+y^4)w=0, x^2+y^2<1 \\ w(x, y)=0, x^2+y^2=1$$

From Green's theorem at $\Omega$ we have that $$\iint_{\Omega}\left (\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right )dxdy=\int_{\partial{\Omega}}(Pdx+Qdy)$$

We choose $$Q=(1+x^2)\frac{\partial{w}}{\partial{x}}, P=-(1+x^2+y^2)\frac{\partial{w}}{\partial{y}}$$

$$\iint_{\Omega}\frac{\partial}{\partial{x}}\left ( (1+x^2)\frac{\partial{w}}{\partial{x}}\right )+\frac{\partial}{\partial{y}}\left ((1+x^2+y^2)\frac{\partial{w}}{\partial{y}}\right )\\ =-\int_{\partial{\Omega}}-(1+x^2+y^2)\frac{\partial{w}}{\partial{y}}dx+(1+x^2)\frac{\partial{w}}{\partial{x}}dy$$

How could I continue?? (Wondering)

 

[I like Serena]

Hi! (Smile)

Logically the next step should be to fill in the boundary, which has $x^2+y^2=1$, and which we can trace with $x=\cos\phi,y=\sin\phi$.
Furthermore, we know that on this boundary, we have $w(x,y)=w(\phi)=0$.
Thus:
$$\d w \phi = \pd w x \d x \phi + \pd w y \d y \phi = 0 \Rightarrow -w_x y + w_y x = 0$$
Although, to be honest, I still don't see how we're supposed to find from this that $w(x,y)=0$ on the interior. (Sweating)

Btw, I think there is a superfluous minus sign. (Worried)
I do see another approach... (Thinking)
If we work out the derivatives, and if we assume $w$ has a maximum $w>0$ in the interior, then it follows that at this maximum $w_x=w_y=0$ and $w_{xx}, w_{yy} \le 0$. This leads to a contradiction. Same thing for a minimum. (Mmm)

 

[mathmari]

Logically the next step should be to fill in the boundary, which has $x^2+y^2=1$, and which we can trace with $x=\cos\phi,y=\sin\phi$.
Furthermore, we know that on this boundary, we have $w(x,y)=w(\phi)=0$.
Thus:
$$\d w \phi = \pd w x \d x \phi + \pd w y \d y \phi = 0 \Rightarrow -w_x y + w_y x = 0$$
Although, to be honest, I still don't see how we're supposed to find from this that $w(x,y)=0$ on the interior. (Sweating)

So, to use the Green's theorem do we have to use spherical coordinates?? (Wondering)

 

[I like Serena]

So, to use the Green's theorem do we have to use spherical coordinates?? (Wondering)

Polar coordinates actually, yes. (Thinking)

 

[mathmari]

I found the following solution in my notes:

View attachment 4460

Could you explain to me the part where $V_x$ is used?? (Wondering)

 

[I like Serena]

I found the following solution in my notes:



Could you explain to me the part where $V_x$ is used?? (Wondering)

Interesting! (Happy)

That's not Green's Theorem but Integration by parts in higher dimensions.
$V_x$ is supposed to be the x-component of the outward facing normal on the boundary, which I think should be $x$ instead of $1$.