I Having problems finding an equation for radioisotope production yield

[fissile_uranium]

TL;DR Summary

I'm trying to find the required target mass for a specific nuclear reaction with a fixed yield and cross-section.

I am trying to get a plot, or a result for target like this:

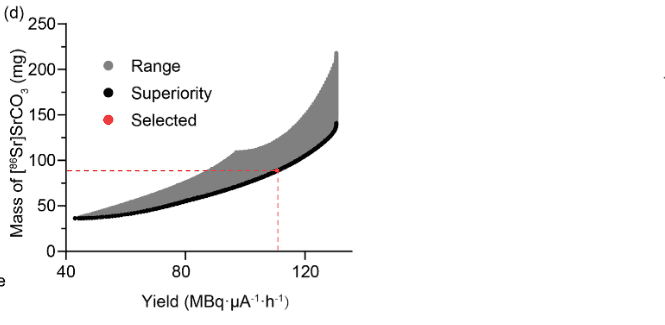
I've found some equations for my requested results, but they are from the same person's articles and I couldn't find another source. I've searched for EOB and TTY calculations but couldn't really do something. Could you give me an easy equation to apply? Also there are equations from this link:
https://www.degruyter.com/document/doi/10.1515/ract-2013-2234/html

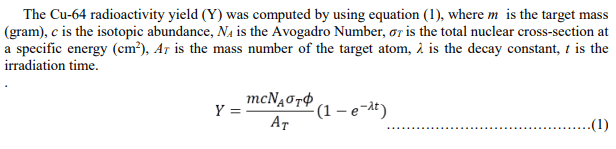
Could you help me with the wanted results? What equation should I use?

Properties:

29.4 TBq
0.05 barns
45 (target molar mass)
59.1 years (produced radionuclide half-life).

 

[mfb]

All parameters in your equation are constants or given except the time, the mass and the beam flux (calculate the decay constant from the half life). The flux you have to find somewhere. For the best rate (minimal target mass) you would assume "infinite irradiation time" ($t\gg\lambda$). That is not realistic with a half life of 59 years, so choose some realistic irradiation time.

 

[fissile_uranium]

@mfb I do not have the flux. And I want to get mass results for 29.4TBq/μA.h, just like the graph on top. But I do not have the equation. Are those real equations that give me mass or should I use another TTY equation?

I actually want something optimal, an optimal mass with an optimal time but to get there I think at first I need the mass information for 1 hour irradiation at 1 μA for the required activity yield. Also is there some way to transform beam current to the beam flux?

Sorry I am very new at these calculations.

 

[mfb]

And I want to get mass results for 29.4TBq/μA.h, just like the graph on top.

Then divide the equation by the flux and the time.
This is elementary algebra, things you should have mastered 10+ years before working on formulas for radioisotope production.

 

[berkeman]

Thread closed temporarily for Moderation...

 

[berkeman]

After some cleanup, the thread is reopened.