Having Trouble Solving Predator-Prey Equations?

[buckmo]

Problem:
x = number of rabbits
y = number of foxes

Accept the usual assumptions involved in predator-prey (Lotka-Volterra) problems.

dx/dt = 0.04x - 0.002xy
dy/dt = -0.08y + 0.0004xy

Initial conditions: 200 rabbits and 10 foxes

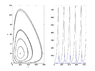
This problem is in a textbook. A graph of the functions x and y when 0 </= t </= 240 is illustrated without showing the functions that are graphed. I am trying to generate those functions.

I am having trouble solving the differential equations. I began by separating variables...

dx/dt = 0.04x - 0.002xy
500(1/x)dx = (20 - y)dt
500 ln(x) = t(20 - y) + C1

Using initial conditions, C1 = 500 ln(200), so

500 ln(x) = t(20 - y) + 500 ln(200)

Solving the other equation in a similar way gives

2500 ln(y) = t(x - 200) + 2500 ln(10)

From here I tried several techniques put found myself painted into a corner. I am thinking I need to rethink the method of solving the equations above. Euler's Method may work to approximate values, but I don't know how to set it up. Suggestions?

Thanks for taking a look.

 

[lurflurf]

You will not be able to solve those in closed form. You cannot separate variables like that because x and y are not independent. You will need to use an approximation method like perturbation or Runge-Kutta. These equations are likely to generate loops, Euler is not very stable and may not loop well. You will be able to find an implicit solution.
hint take the general equation
x'=(b-p y)x
y'=(r x-d)y
show that
p y'+r x'=b r x-d p y

 

[gato_]

Is an analytical solution so useful? The easiest way to proceed with this equation is local analysis.
x&#039;=ax-bxy , y&#039;=-cy+dxy
the important things happen around the points where x'=y'=0, which correspond to (x0,y0)=0, (x0,y0)=(c/d, a/b). Next step is linearizing around those points and obtaining the corresponding jacobian:
(x&#039;,y&#039;)^{T}\approx [a-by_{0},-bx_{0};dy_{0},-c+dx_{0}](x,y)^{T}
From that you can see point (0,0) is unstable, and point (c/d,a/b) is surrounded of oscillations with an approximate frequency of \omega\approx \sqrt(ca)

 

[gato_]

For your problem in particular, the equilibrium point would be (200,20), and the oscillations have a period of about 100. You can see in the figure several phase space trajectories, and a sample time signal simulated

 

[elibj123]

I can give you the solution as an implicit function f(x,y)=0:

using chain rule dy/dt=(dy/dx)*(dx/dt) you obtain the following ODE:

a=0.04,b=0.002,c=0.08,d=0.0004
\frac{dy}{dx}=\frac{0.0004xy-0.08y}{-0.002xy+0.04x}=\frac{0.0004-0.08\frac{y}{x}}{0.04-0.002\frac{x}{y}}<br />

using the substitution z=y/x and dy=x*dz+z:

<br /> x\frac{dz}{dx}+z=\frac{0.0004z-0.08z^{2}}{0.04z-0.002}<br />

<br /> x\frac{dz}{dx}=\frac{0.0024z-0.12z^{2}}{0.04z-0.002}<br />

<br /> \frac{0.04z-0.002}{0.0024z-0.12z^{2}}dz=\frac{dx}{x}<br />

I integrate both sides, using Wolfram Integrator to integrate the monster on the left
and get that

<br /> \frac{-0.003196 log(0.0024-0.12z)-0.00024log(z)}{0.000288}=log(Kx), K&gt;0<br />

substituting back to z=y/x:
<br /> \frac{-0.003196 log(0.0024-0.12\frac{y}{x})-0.00024log(\frac{y}{x})}{0.000288}=log(Kx), K&gt;0<br />

and this is the solution. maybe you can play around with it to get a y=f(x) form of solution