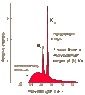It appears to me that you're seeking a scientific justification for associating a particular musical note with Calcium.
The sample in the wikimedia image above is preserved in Argon -- free Calcium is not naturally available on Earth, because it's too reactive, so maybe you're thinking of the Calcium bound in bones and teeth as calcium hydroxyapatite (Ca10[PO4]6[OH]2), or in calcium carbide (CaC2), the anyhdride of acetylene gas.
If you're thinking more along the lines of resonant frequency, such as might be used in a metal detector, you'd have to know what mineral you were trying to find.
If you're looking at spectral lines for a possible basis, you have multiple lines available, as in your NIST table and in the following image (from
https://en.wikipedia.org/wiki/Spectral_line):
If you want to try to start to map the chart's frequency values to audible frequencies, you could proceed something like as follows:
A wavelength of 22000 Å at the high end of your wavelength chart means the low end of the frequency band is 136270000 MHz. Moving the decimal point 12 places to the left gives a low-end audible tone of 136.27 Hz. The shorter end of the chart gives a frequency of 1364100000 MHz. Taking that down 12 decimal orders of magnitude results a high-end audible tone of 1364.10MHz. That preserves the ratio, and brings the frequencies down to audio levels. You then read and interpret the rest of the chart, and find some similarly preserving way to let the other data contribute to the audio realization.
So far there's no valid reason for asserting that this range of audio frequencies is more characteristic of Calcium than of some arbitrarily chosen other element.
Because frequencies are rates, the harmonic mean could provide some usefulness. The harmonic mean of the 2 frequencies is 247.27272727273Hz. That's within the realm of musically usable frequencies. So are the other 2 frequencies. You could do various statistical examinations, such as root-mean square-arithmetic mean-geometric mean-harmonic mean (
RMS-AM-GM-HM) inequality. But you'd have to have a good reason, and I for one don't see a
prima facie basis for a supposition that the NIST data on that table is going to produce anything you could use for your stated purpose. As far as I can tell, there's nothing in that table that can produce a consistent audio property to calcium property mapping.
Something that might actually offer some prospects in that regard, from a credible academic institution, that, like NIST, has due regard for doing real science:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/moseley.html
Taking a quick glance at the Mosely plot of characteristic x-rays, at Ca 20 you can drop the perpendiculars of the 4 points clustered at Calcium, in the mid-high 9 to just over 10 range.
Using the Bohr model of the atom, the points on the plot represent very conspicuous spikes in the absorption or emission spectra at the outermost and next closer-in orbitals, and they plot a highly linear appearance that holds as we go up the elements increasing the atomic numbers in accordance with the periodic table.
Mosely's theory is based on useful and plausible models, well-tested and verified principles, and backed up by good experimental data. His argument includes the tenet that elements can and at very high energies do exhibit frequency spectra that characterize them individually and that they can then be by a legitimate procedure associated with drastically lower frequencies that correspond linearly to their atomic numbers, and retain their characteristic individuation.