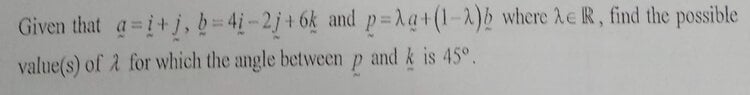MHB Is $\underline{k} = \langle 0,0,1 \rangle$ by Definition in Vector Notation?

  • Thread starter Thread starter Joe20
  • Start date Start date
Click For Summary
The discussion centers on whether the vector notation $\underline{k}$ is defined as $\langle 0,0,1 \rangle$. Participants express uncertainty about the question and seek clarification on the definition of $\underline{k}$. The consensus leans towards confirming that $\underline{k}$ indeed represents the unit vector in the z-direction, which is $\langle 0,0,1 \rangle$. Additional questions regarding the workings and understanding of vector notation are raised. Overall, the conversation emphasizes the importance of clear definitions in vector mathematics.
Joe20
Messages
53
Reaction score
1
Not sure how I should do this question. I have attached my workings with some questions in it. appreciate the help.

View attachment 7978

View attachment 7977
 

Attachments

  • Webp.net-resizeimage12.jpg
    Webp.net-resizeimage12.jpg
    51.3 KB · Views: 93
  • Picture2.jpg
    Picture2.jpg
    14.3 KB · Views: 98
Last edited by a moderator:
Mathematics news on Phys.org
Isn't $\underline{k} = \langle 0,0,1 \rangle$, by definition?
 

Similar threads

Calculating ##\langle zHz \rangle## in different ways
  • · Replies 8 ·
Replies
8
Views
964
MHB Show that the tridiagonal matrix is positive definite
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Dirac Notation for Vectors and Tensors (Neuenschwander's text ....)
  • · Replies 16 ·
Replies
16
Views
3K
Undergrad Geometry and algebraic equations
  • · Replies 4 ·
Replies
4
Views
2K
Prove that ##\langle x, y \rangle = 0 \iff ||x + cy|| \geq ||x||##.
  • · Replies 16 ·
Replies
16
Views
2K
Undergrad More information on the momentum eigenstate in the position basis
  • · Replies 1 ·
Replies
1
Views
1K
Graduate Quantitative description of successive Stern-Gerlach measurements
  • · Replies 1 ·
Replies
1
Views
2K
How to find the eigenvector for a perturbated Hamiltonian?
  • · Replies 13 ·
Replies
13
Views
3K
Undergrad Question about algebraic transformation
  • · Replies 25 ·
Replies
25
Views
3K
Undergrad Ricci notations and visualisation
  • · Replies 10 ·
Replies
10
Views
2K