Help me understand this example of applying Bayes' Theorem

Thread starter dagnir
Start date Nov 3, 2013
Tags

Example Theorem

In summary, Bayes' Theorem is a mathematical formula that calculates the probability of an event based on prior knowledge. It is commonly used in scientific research to update the probability of a hypothesis being true and is applied in fields such as medicine, statistics, and data science. However, it has limitations, such as relying on accurate prior knowledge and assuming independence between events. Bayes' Theorem is also related to Bayesian statistics and is used in machine learning and data science.

Nov 3, 2013

dagnir

I'm reviewing some notes regarding probability, and the section regarding Conditional Probability gives the following example:

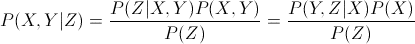
The middle expression is clearly just the application of Bayes' Theorem, but I can't see how the third expression is equal to the second. Can someone please clarify how the two are equal?

Physics news on Phys.org

Nov 3, 2013

mfb

Mentor

Insights Author

The numerator is P(X,Y,Z) in both cases.

Nov 3, 2013

dagnir

Thank you!

1. What is Bayes' Theorem?

Bayes' Theorem is a mathematical formula that describes the probability of an event occurring based on prior knowledge or information. It is named after Reverend Thomas Bayes, who first published the theorem in the 18th century.

2. How is Bayes' Theorem applied in scientific research?

Bayes' Theorem is commonly used in scientific research to update the probability of a hypothesis being true based on new evidence or data. It allows researchers to incorporate prior knowledge and beliefs into their analysis and make more accurate predictions.

3. Can you provide an example of applying Bayes' Theorem?

Sure, let's say we are testing a new drug and want to know its effectiveness in treating a certain disease. We have prior knowledge that the disease affects 1 in 100 people in the general population. We then conduct a clinical trial and find that 80% of the patients who took the drug were cured. Using Bayes' Theorem, we can update the probability of the drug being effective to be 80%.

4. What are the limitations of Bayes' Theorem?

One limitation of Bayes' Theorem is that it relies on accurate and unbiased prior knowledge. If the prior knowledge is incorrect, it can lead to incorrect predictions. Additionally, the theorem assumes that the events are independent, which may not always be the case in real-world situations.

5. How does Bayes' Theorem relate to other statistical methods?

Bayes' Theorem is a foundational concept in Bayesian statistics, which differs from traditional frequentist statistics in its approach to probability and hypothesis testing. Bayes' Theorem is also used in machine learning and data science, where it can be applied to make predictions and classify data.