slakedlime
- 74
- 2
Hello :)
I'm self-studying for my Edexcel Mechanics 2 GCE A Level exam (it's in 10 days :S) and was having lots of trouble with one of the kinematics questions. I've uploaded photos of the problem and my solution for part (a) of the question. I couldn't use the math notation feature on the Physics Forum properly; I hope the photos aren't a problem for anyone!

* When a and b are two perpendicular vectors, a.b = 0.
My working out for part (a) of the question:
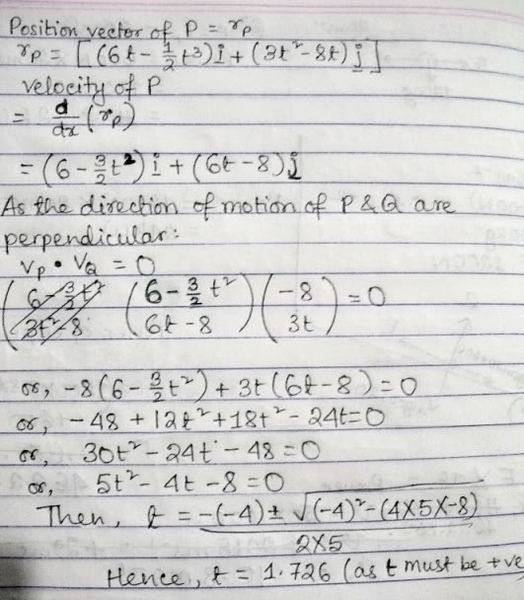
My answer (t = 1.726s) doesn't match with the book's answer of t = 2s. As the book wants the 'instant' when the direction of motion of P is perpendicular to that of Q, I don't think that the book wants me to round off 1.726 to 2.
I'm completely clueless about part (b), so I would really appreciate it if someone could kindly provide some hints to get me in the right direction. I could try solving it then. If you need any further information, please ask and I'll try to provide it. I'm just very, very stumped with this question and have nobody who I can ask. :( Some fresh ideas might really help!
I'm self-studying for my Edexcel Mechanics 2 GCE A Level exam (it's in 10 days :S) and was having lots of trouble with one of the kinematics questions. I've uploaded photos of the problem and my solution for part (a) of the question. I couldn't use the math notation feature on the Physics Forum properly; I hope the photos aren't a problem for anyone!
Homework Statement
Homework Equations
* When a and b are two perpendicular vectors, a.b = 0.
The Attempt at a Solution
My working out for part (a) of the question:
My answer (t = 1.726s) doesn't match with the book's answer of t = 2s. As the book wants the 'instant' when the direction of motion of P is perpendicular to that of Q, I don't think that the book wants me to round off 1.726 to 2.
I'm completely clueless about part (b), so I would really appreciate it if someone could kindly provide some hints to get me in the right direction. I could try solving it then. If you need any further information, please ask and I'll try to provide it. I'm just very, very stumped with this question and have nobody who I can ask. :( Some fresh ideas might really help!