Help requested with translating math into code (Not homework)

[noname12345]

TL;DR

I've found a paper that develops a bunch of equations related to spiral bevel gears. I want to translate those equations into programming code; but I learnt my math a lifetime ago and last used about 1/2 a lifetime ago.

The paper is https://core.ac.uk/display/10365043 (12MB pdf)

My purpose is to construct parametised spiral bevel gears (using OpenSCAD). I know how to produce a correctly formed circular cut (cylindrical) crown gear profile.

My problem is mapping that to a conical surface.

I am looking for someone to help me first understand which of the 85 equations in the paper are the two I think I need, and then help to convert them into code to construct the required affine transform(s).

I see the call for lots of supporting material, but gears are a big subject; and I'd probably end up giving lengthy explanations of wrong things; so I'm hoping it is acceptable to supply further information as required.

The diagrams in the paper are not very clear, so I'll include this which may help in inperpreting some of them.

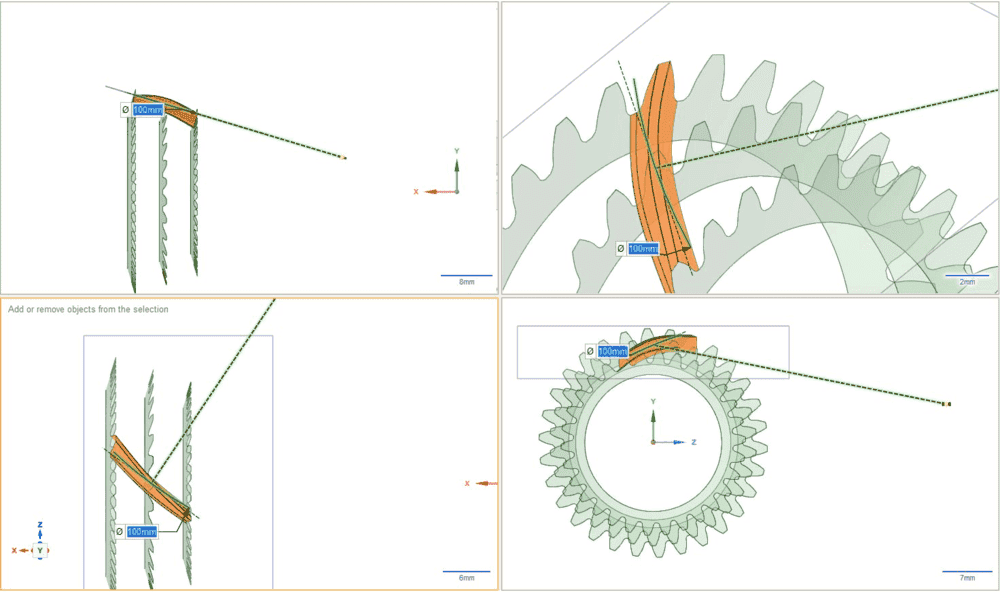
Thanks.

 

[jrmichler]

This question needs to be answered by a gear expert because any programming code will be unique to the particular gear cutting machine. Is this covered in Dudley's Handbook of Practical Gear Design?: https://www.amazon.com/dp/1439866015/?tag=pfamazon01-20. If so, that book would be your best resource if you cannot find a gear expert with specific expertise in this type of gear.

 

[berkeman]

(Thread moved to the ME forum with a redirect left behind in the Differential Geometry forum.)

 

[noname12345]

any programming code will be unique to the particular gear cutting machine.

There is no gear cutting machine involved. The code in question is for generating gear models for use in FEA simulations ONLY.

Is this covered in Dudley's Handbook of Practical Gear Design?: https://www.amazon.com/dp/1439866015/?tag=pfamazon01-20. If so, that book would be your best resource if you cannot find a gear expert with specific expertise in this type of gear.

That book -- a (very old) copy of which is on my bookshelf -- has nothing on differential geometry.
It is only the math -- particularly the differential geometry math -- that I need help with. I am fully conversant with gears and am quite willing to explain any part non-mathematical part of the paper. I am (was:retired) a mechanical engineer; and I know that I will get no help with the mathematics from fellow engineers.

You have effectively consigned MY question to the bin. Thanks a million.

 

[Tom.G]

I had trouble with that linked document (The paper is https://core.ac.uk/display/10365043 (12MB pdf)), that copy may be damaged.

Some government sites will not connect to out-of-country requests, but from the U.S. I had success downloading from:
https://ntrs.nasa.gov/api/citations/19830011867/downloads/19830011867.pdf

And a UK site for downloading the file instead of displaying it in the browser:
https://core.ac.uk/download/pdf/10365043.pdf

The file is too large to attach here.

Cheers,
Tom

 

[berkeman]

(Thread moved to the ME forum with a redirect left behind in the Differential Geometry forum.)

Thread has been moved back to DG.

 

[noname12345]

Too late. The poisonous effect of premature and incorrect redirection persists and will prevent anyone bothering to consider the actual question.
If I could delete it I would. I I could delete my account, I would.

But as this place is still living in the old days, I have to settle for disabling all notifications and deleting all the cookies, and other crap from here locally.

 

[berkeman]

Too late. The poisonous effect of premature and incorrect redirection persists and will prevent anyone bothering to consider the actual question.
If I could delete it I would. I I could delete my account, I would.

But as this place is still living in the old days, I have to settle for disabling all notifications and deleting all the cookies, and other crap from here locally.

No, I think the replies have been limited because you are asking folks to do a rather large amount of work for you for free. What is the end game on this project? Is it just for fun, or for a business project?

 

[Office_Shredder]

Yeah, read this whole paper, look at 85 equations and tell me which one to use sounds like a job, not an interesting intellectual topic.

Your melodramatic response to your thread being moved doesn't make me feel more sympathetic.

I don't even fully understand what you are looking for, just a function that maps a cylinder to a cone?