MHB Help's question at Yahoo Answers regarding quadratic modeling

[MarkFL]

Here is the question:

Pre-calculus, parabola problem?


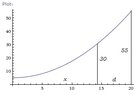
A cable of a suspension bridge is attached to two pillars of height 55 m and has the shape of a parabola whose span is 40 m. the roadway is 5 m below the lowest point of the cable. If an extra support is to be placed where the cable is 30 m above the ground level, find the distance from the nearest pillar where the support is to be placed.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello help,

Let's orient our coordinate axes such that the origin is at the point 5 m below the vertex, or lowest point, of the cable. We know the axis of symmetry will be the $y$ axis, and we know the cable passes through the point $(0,5)$, and so we may write the function $c(x)$ that models the cable with:

$$c(x)=ax^2+5$$

Now, because the span between two pilalrs is 40 m., we therefore also know the cable passes through the point $(20,55)$, and so with this point, we may determine the parameter $a$:

$$c(20)=a(20)^2+5=400a+5=55$$

$$400a=50$$

$$a=\frac{1}{8}$$

Hence:

$$c(x)=\frac{1}{8}x^2+5$$

Now, we want to find the $x$ value(s) such that $c(x)=30$:

$$30=\frac{1}{8}x^2+5$$

$$x^2=200$$

We need only use the positive root by symmetry:

$$x=\sqrt{200}=10\sqrt{2}$$

Now, to find the distance from this value for $x$ and $20$, we simply subtract the $x$-value from 20 to get:

$$d=20-10\sqrt{2}=10\left(2-\sqrt{2} \right)\approx5.85786437626905$$

Here is a diagram of the parabolic function modeling the cable, and the added pillar along with the preexisting pillar:

View attachment 1419