Horizontal lift, or parallel transport

[qinglong.1397]

Hello, everyone!

I'm studying Nakahara's book, Geometry, Topology and Physics and now studying the connection theory. I come across a problem. Please look at the two attachments.

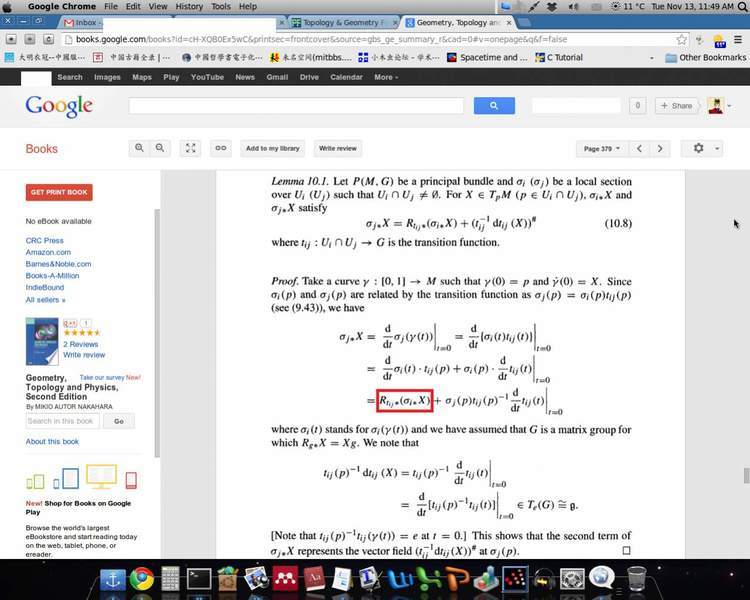
In the attachment

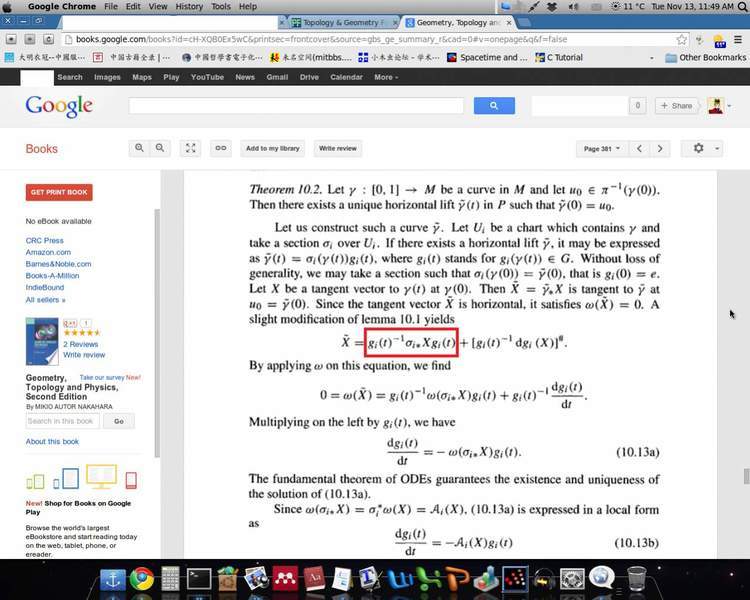, Nakahara said we could use the similar method in the attachment

to get $\tilde X$, but why does the first term have $g_i(t)^{-1}$. According to the first figure, the first term should have the following form

$R_{g_i(t)*}\sigma_{i*}X$

Since $R_{g*}X=Xg$, it becomes

$(\sigma_{i*}X)g_i(t)$

So there shouldn't be $g_i(t)^{-1}$. But why did the author put it there? Thank you!

 

[bloby]

Hello.
When I read this chapter I found this strange. I think it's a mistake. The next equation however is right by (10.3b')

 

[qinglong.1397]

Hello.
When I read this chapter I found this strange. I think it's a mistake. The next equation however is right by (10.3b')

Hey, thanks for your reply! But what is "the next equation", the second equation in the first attachment? If so, I cannot agree with you, because there is no a pullback of a right action.

 

[bloby]

I have to read this chapter again. Here is what I wrote for me:

$$0=\omega\left(\tilde{X}\right)=\omega\left(R_{g_{i}*}\left(\sigma_{i*}X\right)\right)+\omega\left(\left[g_{i}^{-1}dg_{i}\left(X\right)\right]^{\#}\right)=R_{g_{i}}^{*}\omega\left(\sigma_{i*}X\right)+g_{i}^{-1}dg_{i}\left(X\right)=g_{i}^{-1}\omega\left(\sigma_{i*}X\right)g_{i}+g_{i}^{-1}\frac{dg_{i}}{dt}$$

 

[bloby]

$$0=\omega(\tilde{X})=\omega(R_{g_{i}*}(\sigma_{i*}X))+\omega([g_{i}^{-1}dg_{i}(X)]^{\sharp})=R_{g_{i}}^{*}\omega(\sigma_{i*}X)+g_{i}^{-1}dg_{i}(X)=g_{i}^{-1}\omega(\sigma_{i*}X)g_{i}+g_{i}^{-1}\frac{dg_{i}}{dt}$$

 

[qinglong.1397]

$$0=\omega(\tilde{X})=\omega(R_{g_{i}*}(\sigma_{i*}X))+\omega([g_{i}^{-1}dg_{i}(X)]^{\sharp})=R_{g_{i}}^{*}\omega(\sigma_{i*}X)+g_{i}^{-1}dg_{i}(X)=g_{i}^{-1}\omega(\sigma_{i*}X)g_{i}+g_{i}^{-1}\frac{dg_{i}}{dt}$$

Great! Thank you very much!