- #1
jaumzaum
- 434
- 33
Hello guys!
I just started to learn Special Relativity though a Stanford youtube channel, and I had some problems already in the first class
The teacher drew a graph with one spatial dimension (x-axis) and one temporal dimension (t-axis). Where X is the horizontal axis, T is the vertical, both ortogonal. We measure t in seconds and x in light-seconds, so that the line x=t is the light path. Then we introduce a new reference frame. The frame consistis of a person moving to the right with speed v. We prove that the x'and t'axis have the forms written below and we plot them in the graph. Until then, everything fine!
Now we consider the following experiment: I (the one who is moving to the right) have a clock and see in my clock that it has passed 1 second. So, for me, t'=1. When I use the below equations to calculate the time measured by the observer in the X-T system, I find that t=Lt', where L is the Lorentz factor. So t>t'. When I look to the graph, it clearly shows that the "size" of t is smaller than the "size" of t'. The only explanation I have for that is that maybe the graphs don't have the same scale. Is that right? If so, does it really worth it to do graphs like these, if we cannot trust in the size of things? Also, is there a graph that can be constructed in scale between both observers? And lastly, if the graph is not in scale, is there a geometry method to compare the sizes (i.e. find out if t is greater than t' looking to the graph)?
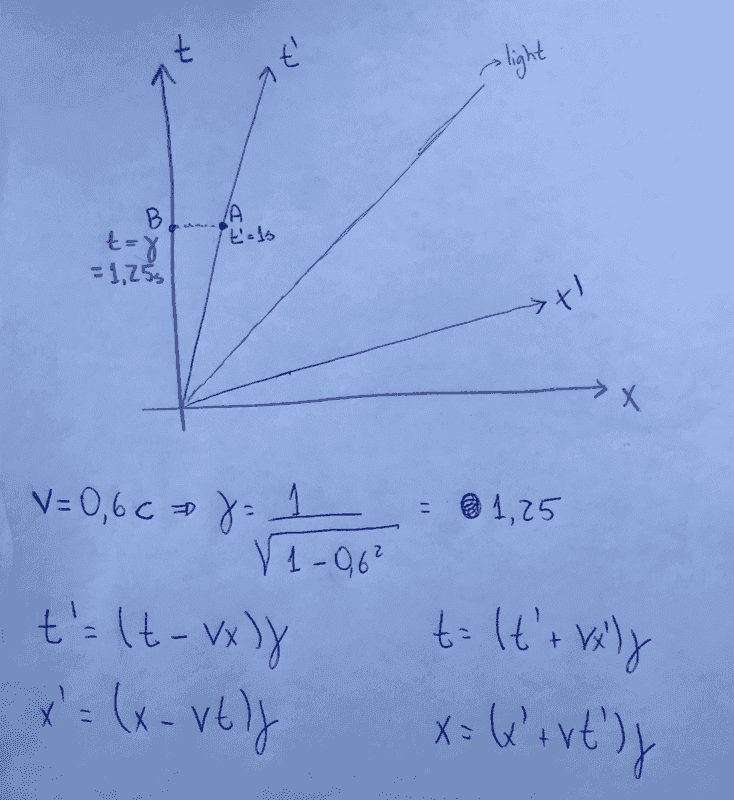
I just started to learn Special Relativity though a Stanford youtube channel, and I had some problems already in the first class
The teacher drew a graph with one spatial dimension (x-axis) and one temporal dimension (t-axis). Where X is the horizontal axis, T is the vertical, both ortogonal. We measure t in seconds and x in light-seconds, so that the line x=t is the light path. Then we introduce a new reference frame. The frame consistis of a person moving to the right with speed v. We prove that the x'and t'axis have the forms written below and we plot them in the graph. Until then, everything fine!
Now we consider the following experiment: I (the one who is moving to the right) have a clock and see in my clock that it has passed 1 second. So, for me, t'=1. When I use the below equations to calculate the time measured by the observer in the X-T system, I find that t=Lt', where L is the Lorentz factor. So t>t'. When I look to the graph, it clearly shows that the "size" of t is smaller than the "size" of t'. The only explanation I have for that is that maybe the graphs don't have the same scale. Is that right? If so, does it really worth it to do graphs like these, if we cannot trust in the size of things? Also, is there a graph that can be constructed in scale between both observers? And lastly, if the graph is not in scale, is there a geometry method to compare the sizes (i.e. find out if t is greater than t' looking to the graph)?