How can a rowing crew be arranged with specific roles for each member?

[Avi1995]

Ques:A boat is to be manned by eight men, of whom 2 can only row on bow side and 1 can only row on stroke side,in how ways can the crew be arranged?



Basic formulae of combinatorics(Permutations and combinations)



Well I do not have good knowledge of boats, but I used the following figure in this problem.

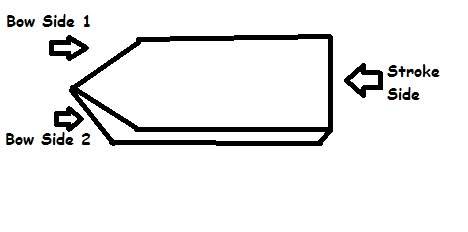
1 will always be on stroke side,
Number of ways in which 2 people can be arranged in bow sides:2
The remaining 5 can be divided into groups of (5,0)(0,5),(4,1)(1,4),(3,2)(2,3) to row on each side,
Total ways are:
2*[2*(5C5)*5!+2*(5C4)*4!+2*(5C3)*3!*2!]

Multiplying all I get=480 way off the answer given in the book which 5760.

 

[tiny-tim]

Hi Avi1995!

a rowing eight has only two sides, with 4 oarsmen on each side

some oarsmen can row on either side (not at the same time, of course!), but some can only row on one side

see this diagram, from http://www.firstandthird.org/tables/rowing/sport.shtml …