Certainly, but before I show you, I should fix up my little typo

L=\sqrt{d^2+h^2-r^2}
sin(A)=\frac{rd+h\sqrt{d^2+h^2-r^2}}{d^2+h^2}
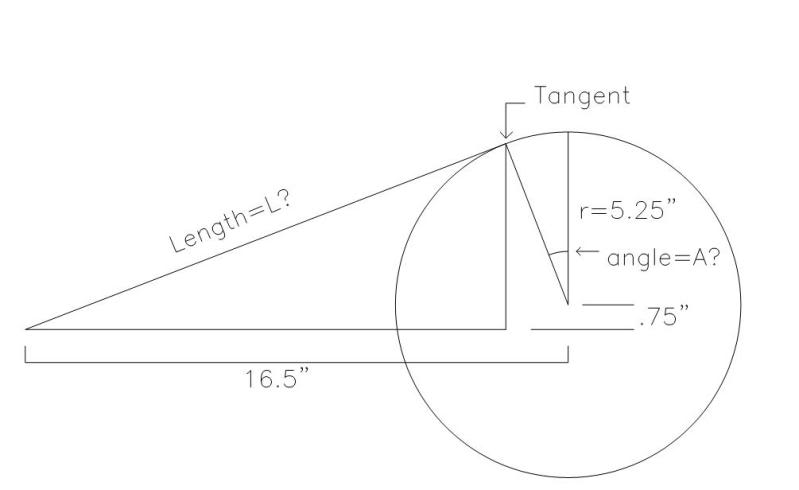
We will let the bottom side of that big triangle with hypotenuse L be m, so the little distance between the centre of the circle and the side of that triangle is d-m.
d-m=rsinA, you can probably figure why this is so for yourself.
There are two parallel lines that are vertical, the radius and the side of that triangle. So the angle between the side of the triangle and the other radius connecting it is A. Also, with a big of filling in angles, the very left point on the triangle subtends an angle A too.
So, cosA=\frac{m}{L} in that big triangle.
Combining these two equations by eliminating m, LcosA=d-rsinA
Now for some algebra:
L\sqrt{1-sin^2A}=d-rsinA
L^2(1-sin^2A)=d^2-2drsinA+r^2sin^2A
L^2sin^2A+r^2sin^2A-2drsinA-L^2+d^2=0
\left(L^2+r^2\right)sin^2A+\left(-2dr\right)sinA+\left(d^2-L^2\right)=0
I put them all in brackets to easily notice that the quadratic formula is going to be used here.
sinA=\frac{2dr\pm\sqrt{4d^2r^2-4(L^2+r^2)(d^2-L^2)}}{2(L^2+r^2)}
substituting L^2=d^2+h^2-r^2
sinA=\frac{2dr\pm\sqrt{4d^2r^2-4(d^2+h^2)(-h^2+r^2)}}{2(d^2+h^2)}
sinA=\frac{2dr\pm\sqrt{4d^2r^2+4d^h^2-4d^2r^2+4h^4-4h^2r^2}}{2(d^2+h^2)}
sinA=\frac{2dr\pm\sqrt{4h^2(d^2+h^2-r^2)}}{2(d^2+h^2)}
sinA=\frac{dr\pm h\sqrt{d^2+h^2-r^2}}{d^2+h^2}
Now to figure out which solution is correct, the plus of minus, I just used simple numbers for d, h and r and found which fits the problem. If anyone could think of a more elegant way I would like to hear about it.
Just as a notice, if you use some random numbers to try, the problem cannot be physically made if d^2+h^2-r^2<0 or, r>\sqrt{d^2+h^2} since it is not possible for the length between the centre of the circle and the end point of the triangle to be shorter than the radius, else the end point of the triangle will somehow be in the circle

So finally, sinA=\frac{rd+h\sqrt{L}}{d^2+h^2}