How Can I Calculate the Probability in a Multi-Level Box System?

[Unconscious]

Good morning,
I have a system that consists of a huge number of boxes, it is not important to know how many, each containing a binary number:

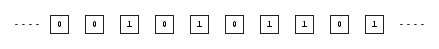
In every cell, the probability that there is a '1' is p, so the probability that there is a '0' is equal to (1-p).
What I do is take them in groups of N and add them up. For each of these sums, I calculate the probability that it is at least M.
So:

if I do not make errors in the reasoning, the probability p' that the generic blue box contains a number greater than M is:

$p' = \sum_{j=M}^N \binom{N}{M}p^j (1-p)^{N-j}$

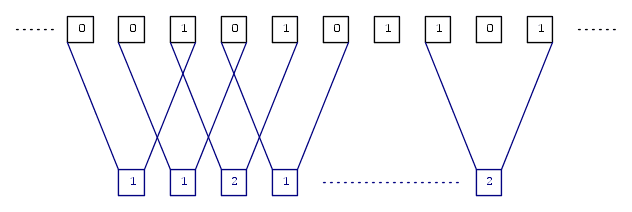
In each of the blue boxes, I insert a '1' if the threshold M has been exceeded (or equaled), otherwise '0'. For example, in the previous drawing (where N = 3) if I use M = 2:

At this point I take another step, and this is where my doubts come from.
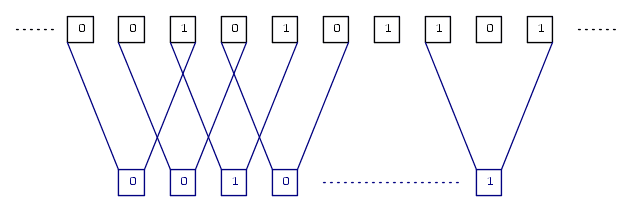
I again cover the blue boxes in groups of N, separately though:

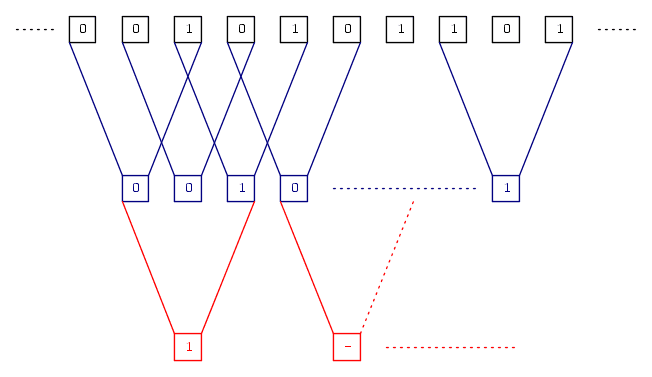
I want to calculate the probability p' that is the probability that in the generic red box there is a number greater than or equal to 1. Surely I can write it like this:

where obviously (1-p'') is the probability that in the generic red box there is a '0'. This is the probability that in N consecutive blue boxes there is always '0'. In my opinion, I cannot simply say that

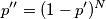because it does not seem to me that the events are independent.

I thought then to 'count' all the cases in my favor, using only the elementary events corresponding to the black boxes of the first row. Since this count is not at all trivial, at least for me, I had Matlab run it, with this code:

M = 4 ;
N = 8 ;
P_in = 1e-2 ;

M_results = zeros(2^(2*N-1),2*N-1);
M_prob = zeros(2^(2*N-1),2*N-1);
for i=2:2*N
    M_results(:,i-1)=repmat([ zeros(2^(2*N-i),1) ; ones(2^(2*N-i),1) ],2^(i-2),1);
    M_prob(:,i-1)=repmat([ (1-P_in)+zeros(2^(2*N-i),1) ; P_in*ones(2^(2*N-i),1) ],2^(i-2),1);
end

Probs = prod(M_prob,2);
P = 0;

for k=1:2^(2*N-1)
bool = 1;
    for j=1:N-1
        bool = bool && sum(M_results(k,j:N+(j-1)))<M;
    end
    if (bool)
        P = P + Probs(k);
    end
end

1-P

The result provided is 0.09562, in the case where N = 8 and M = 4.
I'd be curious to know an opinion on this calculation, do you think I made a mistake or is it all correct?

If you need further clarifications, I am obviously available to provide them.

Thanks in advance.

 

[mfb]

The numbers in the blue box are correlated, indeed. If N is not too big the easiest approach is to go through all options, as you did. For larger N a Monte Carlo approach might be better.

 

[Unconscious]

Ok, thank you.