How can I calculate the union of two rotated rectangles using an algorithm?

[emaybert]

I'm trying to write an algorithm that will take in, as parameters, two rectangles R1 and R2 and calculate their union.
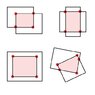
R1 and R2 may be in rotated (independently), one may be completely inside the other, or they may not be overlapping at all.

Example(Image):

View attachment 7700

The algorithm I wrote currently takes in the top-left x,y of each R as well as width/height (rotation not yet considered)

getUnionRect( x1, y1, w1, h1, x2, y2, w2, h2 )
{
  var  rx, ry, rw, rh; //resulting union rectangle (x,y,width,height)
  rx = x2 > x1 ? x2 : x1;
  ry = y2 > y1 ? y2 : y1;
  rw = (x1 < x2 ) ? (x1+w1-x2): (x2+w2-x1)
  rh = (y1 + h1) < (y2 + h2) ? (y1 + h1- y2) : (y2 + h2 - y1) ;
}

This seems to work for very simple cases, but like I said, it (a) does not factor in rotation, nor (b) consider when the union is a 5-sided polygon (see last example,in image).

Any guidance on how this is done mathematically would be greatly appreciated.

I'm not looking for code ( although that would be great ), but just the general mathematical approach to solving.

 

[tkhunny]

First, you appear to be using the wrong word. All your drawings suggest you seek the INTERSECTION, not the UNION. Perhaps your search for a solution will go better with that information.

Second, Have you considered Collision Detection to find any points of intersection?

 

[I like Serena]

Hi emaybert! Welcome to MHB! (Wave)

For starters, we'll need the intersection points of each side of the first rectangle with each side of the second rectangle.
This can be done with for instance the mathematical algorithm here.

Since you've posted in Pre-University Geometry, I'm not sure if this is what you're looking for though.
Can you clarify?

Btw, if we include rotated rectangles, we will also need a representation for them.
One point with width and height won't suffice.
We'll either need an additional angle, or a list of the coordinates of at least 3 of the points.

And as tkhunny already asked, can you clarify if we're talking about a union or an intersection?

 

[emaybert]

Thank you all for replying.

Perhaps my usage of the word "union" was incorrect and "intersection" more appropriate.

I had not considered collision detection, as I assumed that would simply tell me *if* they overlapped, not the polygon defining that overlap.

For both rectangles R1 and R2, I have the following data available:
- top-left coord point (x,y)
- width (pixels)
- height (pixels)
- rotation angle (relative to the x-axis )

So the other 3 points for each rectangle can be computed.

What I'm trying to achieve is to write a (programming) function that:
- takes in R1 and R2 and
- returns P1 - which would be a polygon defining the intersection. ( perhaps an array of (x,y) coordinates )

 

[tkhunny]

To help you along your way, it would be helpful to:
1) Establish a coordinate system.
2) Use the endpoints to determine the equations of each line - all 8 lines.
3) Use whatever method you like to determine the intersections of the lines.
4) You'll have to decide what to do with parallel lines.
5) Decide which intersections actually lie on the line SEGMENT originally given. Throw out the others.

That's the easy part. Any two lines that are not parallel will intersect SOMEWHERE.

6) It is time to test for convexity. This can be a challenge. Two things can help you along...
All intersections that define your intersection are either:
6a) inside one of the original shapes, or
6b) at an intersection of two sides - one from each shape.

That's all I managed off the top or my brainstorming head.
You have some thinking to do. Try it. Test it.

 

[emaybert]

Thank you so much for the feedback. I really appreciate it.
It gave me a new perspective on solving the problem.
I will try what you suggested.
~ed

 

[I like Serena]

Here's a possible algorithm:

Algorithm: Calculate intersection polygon of rotated rectangles
Input: 2 rotated rectangles
Output: list of points of the polygon of the intersection
1.  For each corner point of each rectangle 
2.      If the point is inside the other rectangle
3.          Add point to intersection list
4.  For each edge of rectangle 1
5.      For each edge of rectangle 2
6.          If the edges intersect
7.              Add intersection point to intersection list
8.  Sort points in intersection list
9.  Optionally remove duplicate points
10. Return intersection list

• To figure out if a point $\mathbf p$ is inside a rectangle, we can check:
  $$0 \le \frac{(\mathbf p - \mathbf a) \cdot \mathbf w}{\|\mathbf w\|^2} \le 1
  \quad\land\quad 0 \le \frac{(\mathbf p - \mathbf a) \cdot \mathbf h}{\|\mathbf h\|^2} \le 1
  $$
  where $\mathbf a$ is the corner point of the rectangle, $\mathbf w$ is the vector in the direction of the width, and $\mathbf h$ is the vector in the direction of the height.
• To figure out if and where 2 edges intersect, we can use the algorithm outlined in the first answer here:
  What's the most efficent way to calculate where two line segments intersect?
• To sort the points, we can find the angle of each point with respect to the centroid (average) of all points found, and sort on that angle.

 

[emaybert]

Thank you for this. I really appreciate it. I will give it a go.

 

[I like Serena]

Btw, if you're looking for javascript code, this will do it:

var polygonsIntersect = require('polygons-intersect');
var poly1 = [{x: 10, y: 10}, {x: 10, y: 30}, {x: 30, y: 30}, {x: 30, y: 10}];
var poly2 = [{x: 20, y: 20}, {x: 20, y: 40}, {x: 40, y: 40}, {x: 40, y: 20}];
console.log(polygonsIntersect(poly1, poly2));

See https://www.npmjs.com/package/polygons-intersect.