Undergrad How Can I Improve My Method for Translating Points on Coordinate Axes?

[RichardWattUK]

TL;DR

I need to translate points on coordinate axes as part of a calculation process

Summary: I need to translate points on coordinate axes as part of a calculation process

Hello everyone,

I've created the diagram below to try and explain what I am trying to do as part of an existing software app that's used to generate profiles and programs to drive a CNC machine to grind worm gears.

The worm profile is translated by rotating point "A" (which is on a linear profile) in the diagram below to point "B" (which is on a curved profile more like how it will be when ground by the machine), and this curved profile is later used for some other stages in the calculation process.

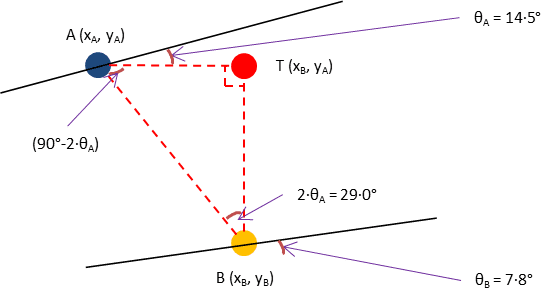The angles θ_A and θ_B represent the angle between the X axis and the outward normal vector from points A and B respectively.

There's an existing routine that uses the Newton-Raphson method to find a rotation angle β to perform this translation and is given the following values:

• Point A (x_A, y_A, θ_A)
• Lead measurement (in mm)
• Projection angle (γ_A)
• Starting values
• Point B (x_B, y_B, θ_B)

The routine calculates a lead angle for point A (α_A): α_A=tan^-1 (Lead/(2π⋅y_A)), where "Lead" is the worm lead measurement.

This routine uses a Newton-Raphson loop to find a value of β that satisfies: C1 ⋅ cos β + C2 ⋅ sin β - C3 = 0 and doesn't always find a solution for all possible combinations of parameters provided by the user.

The values of C1, C2 and C3 are known before starting the iteration by calculating the following:

CA = cos α_A
SA = sin α_A
CG = cos γ_A
SG = sin γ_A
CT = -cos θ_A
ST = sin θ_A

C1 = SA ⋅ CG ⋅ CT
C2 = CA ⋅ CG ⋅ ST
C3 = CA ⋅ SG ⋅ CT

I've found an alternative method to calculate β by solving C1 ⋅ cos β + C2 ⋅ sin β = C3 based on the information in this Quora article.

Once I've got a value for φ from this, I use the following to work out the value of β:

φ = sin^-1 (C1 / √(C1² + C2²))
If |C3 / (C1² + C2²)| Then
β = sin^-1 (C3 / (C1² + C2²)) - φ
Else
β = tan^-1 (C2 / C1) - φ
End If
SB = sin β
CB = cos β

The coordinates of point B are then calculated from:

x_B = β ⋅ Lead / 2π + x_A
y_B = y_A ⋅cos β
θ_B = tan^-1 ((-CA ⋅ CT) / (CA ⋅ CB ⋅ CG ⋅ ST - SA ⋅ SB ⋅ CG ⋅ -CT)) ⋅ (180 / π)

My question is: can anyone see a better way of doing this and/or any improvements that I can make to this method?

 

[fresh_42]

To improve your chances for a reply: Could you just summarize in a list, which values you know, and which you want to calculate? This would make things a lot easier to read (in combination with your picture).

 

[RichardWattUK]

I already know the following values:

• Point A (x_A, y_A, θ_A)
• Lead measurement (in mm)
• Projection angle (γ_A)
• Lead angle (α_A)
• Sines and cosines of angles θ_A, γ_A and α_A
• Coefficients C1, C2, C3

I'm trying to calculate the following values:

• β from solving C1 ⋅ cos β + C2 ⋅ sin β = C3
• Point B (x_B, y_B, θ_B)

Following on from the Quora article, I've been able to solve the equation to get the value of β and get this to work within 0.0001 of the value returned from the existing code that uses the Newton-Raphson method.

I've also been able to work out how to calculate β when $Abs(C3\div\sqrt{C1^2+C2^2})>1$ by using arctan with the appropriate values (I'll update the thread with the equation as I've left the notes at work and I'm typing this at home).