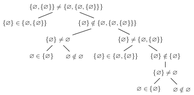
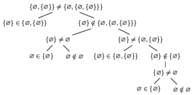
Note that you reduced the problem of proving that $\{ \varnothing, \{ \varnothing \} \}\ne\{ \varnothing, \{ \varnothing, \{ \varnothing \} \} \}$ to showing that $\{ \varnothing \}\ne\varnothing$ and $\{ \varnothing \}\ne\{ \varnothing, \{ \varnothing \}\}$. These are problems of the same type (proving inequalities of sets), so they should be shown in the same way. You started by exhibiting an element $\{ \varnothing \}$ of the first set that you claimed is not an element of the second one. To prove this, it is sufficient to show that $\{\varnothing\}$ is not equal to any of the two elements of the second set. But now $\{ \varnothing \}\ne\varnothing$ can be shown in the same way: $ \varnothing\in\{\varnothing \}$, but $ \varnothing\notin\varnothing$ by definition of $\varnothing$. Similarly, for the second inequality $\{ \varnothing \}\ne\{ \varnothing, \{ \varnothing \}\}$, we have $\{ \varnothing \}\in\{ \varnothing, \{ \varnothing \}\}$, but $\{\varnothing\}\notin\{\varnothing\}$. End of proof.
I am saying that your proof using $\subseteq$
is correct, but it is strange that you used it to disprove $\{ \varnothing \}= \varnothing$ but not the original $\{ \varnothing, \{ \varnothing \} \}=\{ \varnothing, \{ \varnothing, \{ \varnothing \} \} \}$. Note that invoking $\subseteq$ still amounts to exhibiting an element of one set that is not an element of the other.
First, to disprove equality you only have to show $\nsubseteq$. Second, whether it is obvious depends on you and the requirements of the course. I think it is a good idea just once to go all the way to $\varnothing$
You could also start using $\subseteq$ from the start, though this is basically the same proof. Maybe once in life it is OK to go through a very detailed proof, whose outline is shown in the following picture.
View attachment 3314
It has three layers where one needs to prove inequality, and all of them are proven in the same way: by showing some element of one set that does not belong to the other.
After you've done this once or twice, the original statement is indeed obvious because the first set cannot be matched with the second one by changing the order of elements.