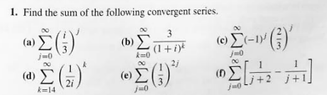How can I solve power series questions 1a, 1c, and 1f?
- Context: MHB
- Thread starter nacho-man
- Start date
Click For Summary
The discussion focuses on solving power series questions 1a, 1c, and 1f, specifically involving complex numbers and geometric series. For question 1a, the series $\displaystyle\sum_{j=0}^{\infty} \left(\frac{i}{3}\right)^j$ is identified as geometric with a sum of $\frac{1}{1-\frac{i}{3}}$, which simplifies to $\frac{9+3i}{10}$. Question 1c is rewritten as $\displaystyle\sum_{j=0}^{\infty}\left(-\frac{2}{3}\right)^j$, while question 1f is recognized as a telescoping sum, leading to a limit evaluation. The use of the power series formula $\frac{1}{1-z} = \sum_{k=0}^{\infty}z^k$ is crucial for these calculations.
PREREQUISITES- Understanding of geometric series and convergence criteria
- Familiarity with complex numbers and their properties
- Knowledge of power series and their summation techniques
- Ability to manipulate algebraic expressions involving complex numbers
- Study the properties of geometric series and their convergence
- Learn about complex number manipulation and conjugates
- Explore telescoping series and their applications in calculus
- Review the derivation and application of the power series formula $\frac{1}{1-z} = \sum_{k=0}^{\infty}z^k$
Students and educators in mathematics, particularly those focusing on calculus and complex analysis, will benefit from this discussion. It is especially relevant for anyone tackling power series and their applications in problem-solving.
Similar threads
- · Replies 2 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 11 ·
- · Replies 1 ·
- · Replies 3 ·
- · Replies 5 ·