Poetria
- 267
- 42
- Homework Statement
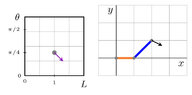
- Let M be the matrix ##\begin{pmatrix}1&-1\\ 0&1\\\end{pmatrix}##. Suppose we move the controller slightly, such that ##\Delta L## increases by 0.2 and ##\Delta \theta## increases by 0.1 . This will move the robot's x and y coordinates by ##\Delta x## and ##\Delta y## respectively. Which of the following vectors closely approximates ##\begin{pmatrix} \Delta x \\ \Delta y \end{pmatrix}## ?
- Relevant Equations
- ##M^{-1}\begin{pmatrix} 0.2 \\ 0.1 \end{pmatrix}##
##M \begin{pmatrix} 0.2 \\ 0.1\end{pmatrix}##
##\begin{pmatrix} 0.2 \\ 0.1 \end{pmatrix}##
If I understand this correctly, this is the right answer: ##M \begin{pmatrix} 0.2\\ 0.1\end{pmatrix}##
There is an inverse matrix in the next question:
Continuing with the previous problem, let ##\vec v = M^{-1} \begin{pmatrix} 0.2\\ 0.1\end{pmatrix}##, where ##M^{-1}## is the inverse matrix of M . Let ##\vec v_1## and ##\vec v_2## be the components of ##\vec v## . Which of the following is the correct interpretation for ##\vec v##?
I think this may be the right answer:
If we increase L by ##\vec v_1## and increase ##\theta## by ##\vec v_2## , then the robot will move 0.2 to the right and 0.1 up.
At first I thought the following choice was correct:
If we increase L by 0.2 and increase ##\theta## by 0.1 , then the robot will move ##\vec v_1## to the right and ##\vec v_2## up.
There is an inverse matrix in the next question:
Continuing with the previous problem, let ##\vec v = M^{-1} \begin{pmatrix} 0.2\\ 0.1\end{pmatrix}##, where ##M^{-1}## is the inverse matrix of M . Let ##\vec v_1## and ##\vec v_2## be the components of ##\vec v## . Which of the following is the correct interpretation for ##\vec v##?
I think this may be the right answer:
If we increase L by ##\vec v_1## and increase ##\theta## by ##\vec v_2## , then the robot will move 0.2 to the right and 0.1 up.
At first I thought the following choice was correct:
If we increase L by 0.2 and increase ##\theta## by 0.1 , then the robot will move ##\vec v_1## to the right and ##\vec v_2## up.