How can we interpret the inverse matrix of a robot's arm?

[Poetria]

Homework Statement

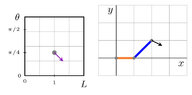
Let M be the matrix $\begin{pmatrix}1&-1\\ 0&1\\\end{pmatrix}$. Suppose we move the controller slightly, such that $\Delta L$ increases by 0.2 and $\Delta \theta$ increases by 0.1 . This will move the robot's x and y coordinates by $\Delta x$ and $\Delta y$ respectively. Which of the following vectors closely approximates $\begin{pmatrix} \Delta x \\ \Delta y \end{pmatrix}$ ?

Relevant Equations

$M^{-1}\begin{pmatrix} 0.2 \\ 0.1 \end{pmatrix}$
$M \begin{pmatrix} 0.2 \\ 0.1\end{pmatrix}$
$\begin{pmatrix} 0.2 \\ 0.1 \end{pmatrix}$

If I understand this correctly, this is the right answer: $M \begin{pmatrix} 0.2\\ 0.1\end{pmatrix}$

There is an inverse matrix in the next question:
Continuing with the previous problem, let $\vec v = M^{-1} \begin{pmatrix} 0.2\\ 0.1\end{pmatrix}$, where $M^{-1}$ is the inverse matrix of M . Let $\vec v_1$ and $\vec v_2$ be the components of $\vec v$ . Which of the following is the correct interpretation for $\vec v$?

I think this may be the right answer:
If we increase L by $\vec v_1$ and increase $\theta$ by $\vec v_2$ , then the robot will move 0.2 to the right and 0.1 up.

At first I thought the following choice was correct:
If we increase L by 0.2 and increase $\theta$ by 0.1 , then the robot will move $\vec v_1$ to the right and $\vec v_2$ up.

 

[FactChecker]

Is the mathematical notation of a robotic arm so standardized that we are supposed to know what all this means? I don't.

 

[Poetria]

Sorry, I should have sent an image.

 

[Poetria]

Or is my question silly? :(

 

[Poetria]

Or is my question silly? :(

Anyway I got it right. :)