How do evaluate this limit because i will get 2.6667 and divide by -144

[Teh]

My Work:

View attachment 6111

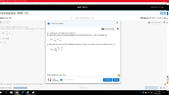
How do evaluate this limit because i will get 2.6667 and divide by -144 it will get me 55.38446...
I know that the answer is WRONG but I can't figure it out.
Then after that i have to plug in into tangent line y-f(a) = Mtan(x-a)

what i am doing wrong.

The Problem:
View attachment 6110

 

[evinda]

How do evaluate this limit because i will get 2.6667 and divide by -144 it will get me 55.38446...
I know that the answer is WRONG but I can't figure it out.
Then after that i have to plug in into tangent line y-f(a) = Mtan(x-a)

what i am doing wrong.
The problem:

Do we have at the denominator $\boldsymbol + 4+12 \sqrt{x}$ ? If so then by substitung at $x$ the value $\frac{1}{9}$ and since $\sqrt{9}=3$, the limit is equal to $\frac{-144}{\frac{1}{3}\left( 4+\frac{12}{3}\right)}=\frac{-144 \cdot 3}{\left( 4+\frac{12}{3}\right)}=\frac{-144 \cdot 3}{\frac{24}{3}}=\frac{-144 \cdot 9}{24}=-6 \cdot 9=-54$.

Also it holds that $\left( \frac{1}{\sqrt{x}}\right)'=-\frac{1}{2 x^{\frac{3}{2}}}$.

 

[MarkFL]

Because you speak of limits, I am assuming you are to use the definition:

$$f'(x)\equiv\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$

where:

$$f(x)=\frac{4}{\sqrt{x}}$$

So, let's look at what we'll be taking the limit of:

$$\frac{\dfrac{4}{\sqrt{x+h}}-\dfrac{4}{\sqrt{x}}}{h}=4\frac{\sqrt{x}-\sqrt{x+h}}{h\sqrt{x(x+h)}}=-\frac{4}{\sqrt{(x(x+h))}\left(\sqrt{x}+\sqrt{x+h}\right)}$$

So, we now have a determinate form, and we can state:

$$f'(x)=-4\lim_{h\to0}\frac{1}{\sqrt{(x(x+h))}\left(\sqrt{x}+\sqrt{x+h}\right)}$$

Can you proceed to determine the limit now?

 

[Teh]

What the..HOW lol dang it ahhhh... -.- let me see what you did

- - - Updated - - -

Because you speak of limits, I am assuming you are to use the definition:

$$f'(x)\equiv\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$

where:

$$f(x)=\frac{4}{\sqrt{x}}$$

So, let's look at what we'll be taking the limit of:

$$\frac{\dfrac{4}{\sqrt{x+h}}-\dfrac{4}{\sqrt{x}}}{h}=4\frac{\sqrt{x}-\sqrt{x+h}}{h\sqrt{x(x+h)}}=-\frac{4}{\sqrt{(x(x+h))}\left(\sqrt{x}+\sqrt{x+h}\right)}$$

So, we now have a determinate form, and we can state:

$$f'(x)=-4\lim_{h\to0}\frac{1}{\sqrt{(x(x+h))}\left(\sqrt{x}+\sqrt{x+h}\right)}$$

Can you proceed to determine the limit now?

for my problem i won't be using f(a+h) - f(h) instead Ill be using this...View attachment 6112but is there any different?

 

[evinda]

These are two different definitions. Both give the same result.

 

[Teh]

These are two different definitions. Both give the same result.

ahh...okay thank you very much

 

[MarkFL]

What I gave and the example you have been given use different notation, but they are equivalent. They are using:

$$a=x+h$$

So, as $h\to0$ we have $a\to x$. They are telling you to use:

$$f'(x)\equiv\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$$

So, using the given definition of $f$, what we are taking the limit of is:

$$\frac{\dfrac{4}{\sqrt{x}}-\dfrac{4}{\sqrt{a}}}{x-a}=\frac{4\left(\sqrt{a}-\sqrt{x}\right)}{(x-a)\sqrt{ax}}=-\frac{4}{\sqrt{ax}(\sqrt{a}+\sqrt{x})}$$

And so you now have the determinate form:

$$f'(x)=-4\lim_{x\to a}\frac{1}{\sqrt{ax}(\sqrt{a}+\sqrt{x})}$$