How do I construct this Triangle?

  • Context: MHB 
  • Thread starter Thread starter schunck
  • Start date Start date
  • Tags Tags
    Triangle
Click For Summary
SUMMARY

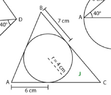
The discussion focuses on constructing triangle "J" using basic geometric tools: a protractor, ruler, compass, and pencil. A key insight shared is that the two tangents from a point to a circle are equal in length, which aids in the construction process. Specifically, line segment AB measures 13cm, and a circle with a radius of 4cm touches this line at a point 6cm from point A. Understanding these relationships allows for the successful construction of the triangle without needing to calculate angles.

PREREQUISITES
  • Basic knowledge of geometric constructions
  • Understanding of tangents to circles
  • Familiarity with using a protractor and compass
  • Ability to measure and draw accurately with a ruler
NEXT STEPS
  • Research geometric constructions involving circles and tangents
  • Learn about the properties of tangents and their applications in triangle construction
  • Explore techniques for constructing triangles without angle measurements
  • Practice using a compass and protractor for accurate geometric drawings
USEFUL FOR

Students learning geometry, educators teaching geometric constructions, and anyone interested in improving their skills in manual drafting and geometric problem-solving.

schunck
Messages
2
Reaction score
0
I have to construct the triangle "J" only using protractor, ruler, compass and pencil. But I can't seem to find a way to figure out the angles. Please help.

View attachment 6315
 

Attachments

  • Skærmbillede 2017-01-11 kl. 11.36.03.png
    Skærmbillede 2017-01-11 kl. 11.36.03.png
    18.7 KB · Views: 96
Last edited:
Mathematics news on Phys.org
schunck said:
I have to construct the triangle "J" only using protractor, ruler, compass and pencil. But I can't seem to find a way to figure out the angles. Please help.
Hi schunck, and welcome to MHB!

Just to get you started, the two tangents from a point to a circle have the same length. So the line $AB$ is 13cm long, and a circle of radius 4cm touches it at a distance 6cm from $A$. Can you take it from there? (You don't need to know the angles.)
 
Of course. Thx
 

Similar threads

High School Constructing a Line Segment Equal to a Circle's Circumference?
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Given a triangle ABC, on which side of the triangle does the point D lie?
  • · Replies 6 ·
Replies
6
Views
2K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Can an Ellipse Help Solve the Scalene Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
MHB [ASK] Find the ratio of the area of triangle BCH and triangle EHD
  • · Replies 4 ·
Replies
4
Views
2K
High School Find triangles with areas that are integers
  • · Replies 20 ·
Replies
20
Views
4K
Undergrad Possible simple formula for ellipse circumference
  • · Replies 6 ·
Replies
6
Views
3K
MHB From a sketch to the compass ; Geometric construction
  • · Replies 8 ·
Replies
8
Views
2K
MHB Length of sides of right triangle with 1 angle and 1 side
  • · Replies 2 ·
Replies
2
Views
2K
MHB Show that angle AXC=angle ACB; geometric construction
  • · Replies 10 ·
Replies
10
Views
3K