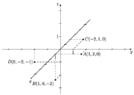Concerning problem 1), it is impossible to recover coordinates of the shown point from a two-dimensional picture. That is, there is an infinite number of 3D points that, when drawn on a plane, would fall into the same position. However, we are also given four options, and of those only one corresponds to the required point.
View attachment 2432
The most reliable way to find the answer is to draw all four points. To draw a point with coordinates $(x_0,y_0,z_0)$ start with the origin, then move in the direction of the $x$ axis by $x_0$ (in the picture, this means moving bottom left for positive $x_0$), then move in the direction of the $y$ axis by $y_0$ (right for positive $y_0$) and finally in the direction of the $z$ axis by $z_0$ (up for positive $z_0$). But one can also see that the required point has a negative $z$ coordinate, and there is only one corresponding option.
Problem 2)
View attachment 2433
Problems 3) and 4) are easier because we have lines connecting the point with the coordinate axes. For 3), we first go up to the $xy$ plane and then left to the $x$ axis. We arrive at $x=4$. Similarly, going up and then towards the $y$ axis we arrive at $y=4$. Finally, going towards the $xy$ plane (where $z=0$) required going up 1 unit, so the $z$ coordinate is $-1$. Note that each time we move along a straight line segment, it must be parallel to one of the axes. The answer to 4) is $(-1,2,-4)$.