zak100
- 462
- 11
Originally posted in a non-homework forum section
Hi,
I got a question from a book to find the area of a Quadrilateral. I divided the quadrilateral into two triangles but answer is not correct. Some body please guide me.
I am uploading my work in a attached file.
Zulfi.
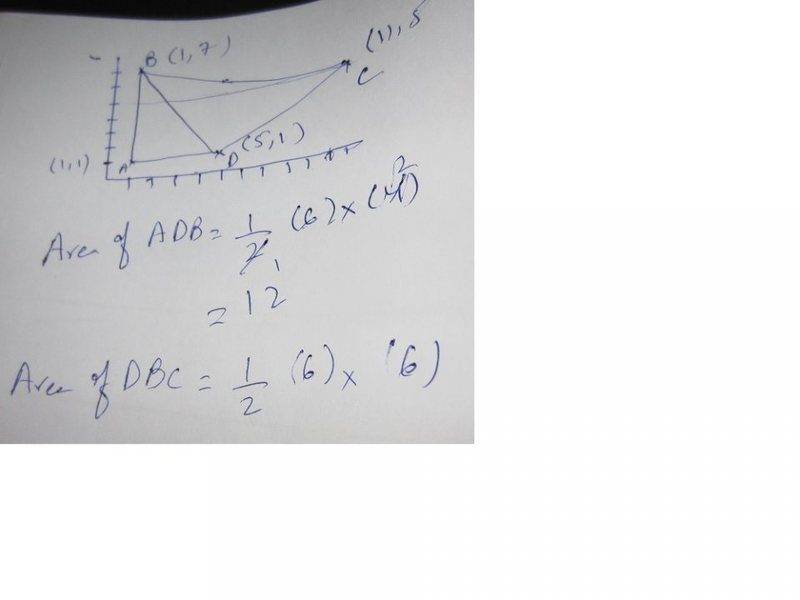
I got a question from a book to find the area of a Quadrilateral. I divided the quadrilateral into two triangles but answer is not correct. Some body please guide me.
I am uploading my work in a attached file.
Zulfi.