How do I find the value of delta in a delta epsilon proof using a graph?

[karush]

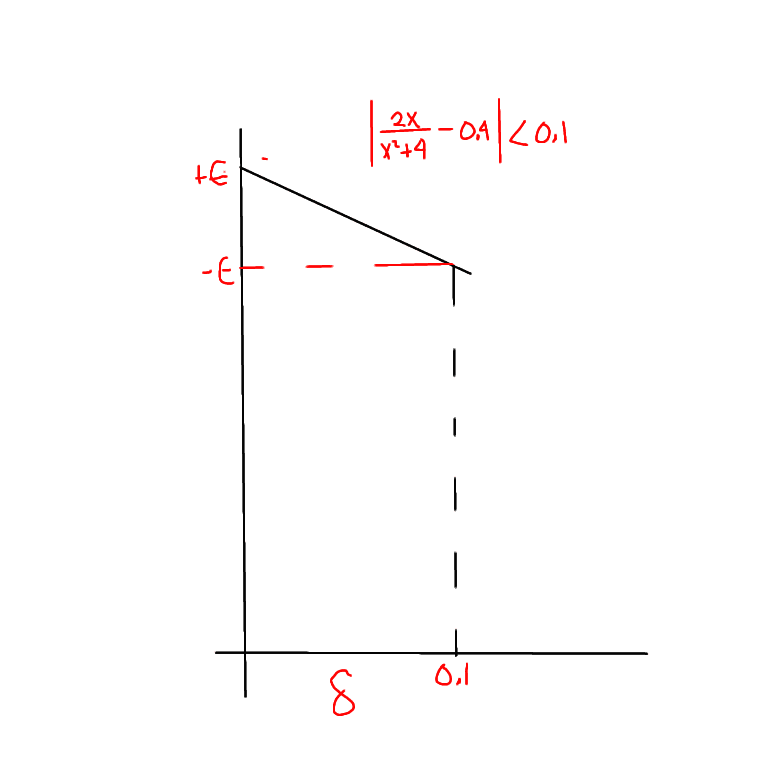
Find a graph to a number $\delta$ such that
$$\textit{if }
|x-1|<\delta
\textit{ then }
\left|\dfrac{2x}{x^2+4}-0.4\right|<0.1
$$

ok I always had a very hard time doing these I did look at some examples but still ?
did a ibispaint drawing to start basically it looks like we are finding the dimenstions of box given the parameters

 

[I like Serena]

Let's draw the function $\frac{2x}{x^2+4}$.

\begin{tikzpicture}[scale=5]
\draw[help lines] (0,0) grid[step=0.1] (2,0.5);
\draw[-latex] (-0.2,0) -- (2.1,0);
\draw[-latex] (0,-0.1) -- (0,0.6);
\draw foreach \i in {0.7,1,2} { (\i,0.5) -- (\i,0) node[ below ] {$\i$} };
\draw foreach \i in {0.3,0.4,0.5} { (2,\i) -- (0,\i) node[ left ] {$\i$} };
\draw[domain=-0.2:2.1, variable=\x, blue, ultra thick] plot ({\x}, {2*(\x)/((\x)^2+4)}) node[ right ] {$\frac{2x}{x^2+4}$};
\end{tikzpicture}

 

[karush]

So you are saying the transformations of $- 0.4$ and the ABS are not critical for the proof

I think I see how the rest of the calculations would go

 

[I like Serena]

So you are saying the transformations of $- 0.4$ and the ABS are not critical for the proof

I think I see how the rest of the calculations would go

They are relevant.
Let $f(x)=\frac{2x}{x^2+4}$.
Then we have $|f(x)-0.4|<0.1$ and $f(1)=0.4$.
It follows that we must have $0.3 < f(x) < 0.5$, and I've drawn the corresponding horizontal lines at $y=0.3$ and $y=0.5$ in the picture.
Now we need to find a minimum and maximum $x$ around $x=1$ such that the function is between those horizontal lines.
In the picture we can see that if $0.7 < x < 2$ that the function will indeed be between those lines.

That leaves finding $\delta$ such that if $|x-1|<\delta$ that we will have $0.7 < x < 2$.

 

[karush]

They are relevant.
Let $f(x)=\frac{2x}{x^2+4}$.

They are relevant.
Let $f(x)=\frac{2x}{x^2+4}$.
Then we have $|f(x)-0.4|<0.1$ and $f(1)=0.4$.
It follows that we must have $0.3 < f(x) < 0.5$, and I've drawn the corresponding horizontal lines at $y=0.3$ and $y=0.5$ in the picture.
Now we need to find a minimum and maximum $x$ around $x=1$ such that the function is between those horizontal lines.
In the picture we can see that if $0.7 < x < 2$ that the function will indeed be between those lines.

That leaves finding $\delta$ such that if $|x-1|<\delta$ that we will have $0.7 < x < 2$.

Then we have $|f(x)-0.4|<0.1$ and $f(1)=0.4$.
It follows that we must have $0.3 < f(x) < 0.5$, and I've drawn the corresponding horizontal lines at $y=0.3$ and $y=0.5$ in the picture.
Now we need to find a minimum and maximum $x$ around $x=1$ such that the function is between those horizontal lines.
In the picture we can see that if $0.7 < x < 2$ that the function will indeed be between those lines.

That leaves finding $\delta$ such that if $|x-1|<\delta$ that we will have $0.7 < x < 2$.

Mahalo Much
I'm need to do a lot more of these to really have it down cold

I tried to make the boundary lines dashed and just up the the graph but that must be separate from the for each call?