haha0p1
- 46
- 9
- Homework Statement
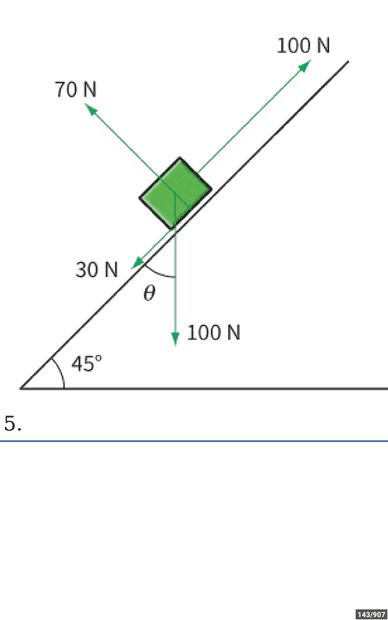
- The figure shows the forces acting on a box that is being pushed up a slope. Calculate the work done by each force if the box moves 0.50m up the slope.
- Relevant Equations
- Work done= Force×Direction of force
I have found the work done for 100 N, 70 N and 30 N force, but I don't know how to find work for 100 N force that is acting downwards.
Force 70N:
W=F×d = 70 ×0=0 Nm (Force is perpendicular to the distance moved)
100 N force:
W=F×d=100×0.5=50 Nm
30N force:
30×-.5= -15Nm.
Please check whether these answers are right and also tell how to find the work done for 100 N force acting downwards.
Force 70N:
W=F×d = 70 ×0=0 Nm (Force is perpendicular to the distance moved)
100 N force:
W=F×d=100×0.5=50 Nm
30N force:
30×-.5= -15Nm.
Please check whether these answers are right and also tell how to find the work done for 100 N force acting downwards.