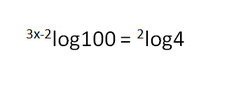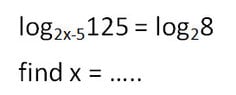- #1
How do I Solve a Basic Logarithm Problem?
- Context: MHB
- Thread starter susanto3311
- Start date
-
- Tags
- Logarithm
Click For Summary
SUMMARY
The discussion focuses on solving logarithmic equations, specifically the equations \(\log_{3x-2}100 = \log_24\) and \(\log_{2x-5}125 = \log_28\). The solutions derived are \(x = 4\) for the first equation and \(x = 5\) for the second. The participants clarify the logarithmic notation and provide step-by-step solutions, demonstrating the application of logarithmic properties to isolate \(x\).
PREREQUISITES- Understanding of logarithmic functions and properties
- Familiarity with solving algebraic equations
- Knowledge of logarithmic notation and bases
- Basic skills in manipulating exponents
- Study the properties of logarithms, including change of base and product/quotient rules
- Practice solving logarithmic equations with different bases
- Explore advanced logarithmic applications in exponential growth and decay problems
- Learn about the graphical representation of logarithmic functions
Students, educators, and anyone seeking to improve their understanding of logarithmic equations and their applications in mathematics.
- #2
soroban
- 191
- 0
I've never seen logarithms written like that . . .susanto said:
\begin{array}{ccc}\text{We have:} & \log_{3x-2}100 \:=\:\log_24 \\<br /> & \log_{3x-2}100 \:=\:2 \\<br /> & (3x-2)^2 \:=\:100 \\<br /> & 3x-2 \:=\:10 \\<br /> & 3x\:=\:12 \\<br /> & x \:=\:4<br /> \end{array}
- #3
- 2,020
- 843
Is this supposed to be [math]\text{log}_{100}(3x - 2) = \text{log}_4 (2)[/math]?susanto3311 said:
-Dan
- #4
susanto3311
- 73
- 0
hi...
what is finally for x?
what is finally for x?
- #5
susanto3311
- 73
- 0
hi soroban...
thank, but how about this...
\begin{array}{ccc}\text{We have:} & \log_{2x-5}125 \:=\:\log_28 \\<br /> <br /> - - - Updated - - -<br /> <br /> <blockquote data-attributes="member: 703424" data-quote="soroban" data-source="post: 6750174" class="bbCodeBlock bbCodeBlock--expandable bbCodeBlock--quote js-expandWatch"> <div class="bbCodeBlock-title"> soroban said: </div> <div class="bbCodeBlock-content"> <div class="bbCodeBlock-expandContent js-expandContent "> I've never seen logarithms written like that . . .<br /> <br /> \begin{array}{ccc}\text{We have:} &amp; \log_{3x-2}100 \:=\:\log_24 \\<br /> &amp; \log_{3x-2}100 \:=\:2 \\<br /> &amp; (3x-2)^2 \:=\:100 \\<br /> &amp; 3x-2 \:=\:10 \\<br /> &amp; 3x\:=\:12 \\<br /> &amp; x \:=\:4<br /> \end{array} </div> </div> </blockquote><br /> hi soroban...
thank, but how about this...
\begin{array}{ccc}\text{We have:} & \log_{2x-5}125 \:=\:\log_28 \\<br /> <br /> - - - Updated - - -<br /> <br /> <blockquote data-attributes="member: 703424" data-quote="soroban" data-source="post: 6750174" class="bbCodeBlock bbCodeBlock--expandable bbCodeBlock--quote js-expandWatch"> <div class="bbCodeBlock-title"> soroban said: </div> <div class="bbCodeBlock-content"> <div class="bbCodeBlock-expandContent js-expandContent "> I've never seen logarithms written like that . . .<br /> <br /> \begin{array}{ccc}\text{We have:} &amp; \log_{3x-2}100 \:=\:\log_24 \\<br /> &amp; \log_{3x-2}100 \:=\:2 \\<br /> &amp; (3x-2)^2 \:=\:100 \\<br /> &amp; 3x-2 \:=\:10 \\<br /> &amp; 3x\:=\:12 \\<br /> &amp; x \:=\:4<br /> \end{array} </div> </div> </blockquote><br /> hi soroban...
Attachments
- #6
soroban
- 191
- 0
\begin{array}{cc}\log_{2x-5}125 \:=\: \log_28 \\<br /> \log_{2x-5}125 \:=\:3 \\<br /> (2x-5)^3 \:=\:125 \\<br /> 2x-5 \:=\: 5 \\<br /> 2x \:=\: 10 \\<br /> x \:=\:5<br /> \end{array}susanto3311 said:
- - Updated - - -
Similar threads
Undergrad
Logarithmic scale - interpolation
- · Replies 2 ·
- · Replies 2 ·
High School
How does one draw a logarithmic scale?
- · Replies 20 ·
- · Replies 7 ·
High School
Issue With Algebra of Logarithms
- · Replies 8 ·
- · Replies 17 ·
- · Replies 6 ·
- · Replies 4 ·
- · Replies 1 ·