RingNebula57
- 56
- 2
How can we relate mathematically the time interval in which a planet is in retrograde motion and the devided distances from the sun of the planets ?
My first drawing was this:
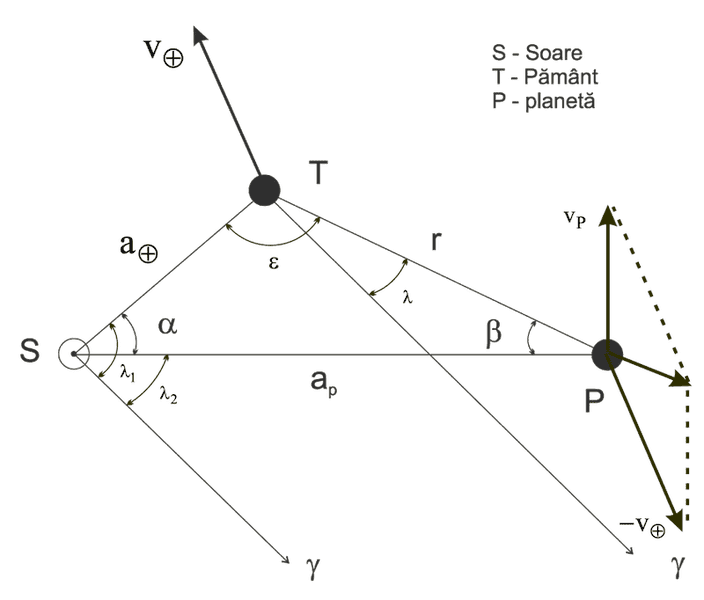 Where S is thee sun , P is the planet, T si the Earth. The v's are the corespondent speeds
Where S is thee sun , P is the planet, T si the Earth. The v's are the corespondent speeds
If we take a look at it we can say that:r x cos(lambda)= ap x cos(labda2) - ao x cos(lambda1) , same for sine
What next?
Oh, and gamma is the vernal point
My first drawing was this:
If we take a look at it we can say that:r x cos(lambda)= ap x cos(labda2) - ao x cos(lambda1) , same for sine
What next?
Oh, and gamma is the vernal point