How Do You Divide a Dome into Equal Pie-Shaped Sections for a Mural?

[fauxtex]

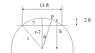
I am an artist, I know a little about math but apparently not enough and I need some help. I am painting a mural on a domed ceiling. The dome is circular, it is 14' in diameter and gradually goes up to 2' high in the center. I need to "cut" this dome into 6 or 8 equal "pie" shapes in order to make a template to transfer my design onto the ceiling. I am stumped as to how to figure the exact shape and size of each of these pieces. Can anyone help me out? Please?
No, I'm not smarter than a fifth grader!

 

[StatusX]

If it's a spherical dome, you won't be able to lay a flat piece of paper on it (this is the reason maps of the Earth are distorted). The best you can do is approximate, and the smaller each piece is, the better it will fit. I'd suggest just experimenting with a smaller sphere.

 

[fauxtex]

I do believe that I can lay a flat piece of paper on it but it has to be cut into a shape that has curved sides. Kind of like a top of a globe flattened out or a flat map of the world that has equal longitude lines with curved sides. (I'm talking about the world maps that look cut up into 'slices", If you cut the flat map of the world on the lines you could wrap it around a globe) I want to cut the dome into 6 or 8 equal sizes. I am painting the same thing on each part of the ceiling though so I only need one for a template. There must be some kind of formula to figure these shapes. No?

 

[Moo Of Doom]

Since it is 14' in diameter, but only 2' high, it can't be spherical. Anyway, it's not a singly curved surface, so paper won't nicely conform to it.

 

[fauxtex]

Ok, Maybe I'm not wording it correctly. Let's say it is a 14' diameter round pool and it slopes to 2' deep in the center. I would like to divide it into 8 equal size and shaped pieces. (Starting in the center and cutting out to the edge similar to a pie, I know they won't have straight edges though) With out having the pool in front of me, How do I figure out how big and what shape the peices will be? Anyone?

 

[StatusX]

Actually they will have straight edges, and that's part of the problem. For example, if you take the triangle cut out by the equator and two lines of longitude such that the angle they make at the north pole is 90 degrees, then you have a triangle with 3 straight sides and 3 right angles, which is impossible in a plane.

You could find the lengths of the sides you want and the angles between them with some simple but tedious geometry (with some assumptions about what the shape is, like whether it's a spherical cap), but you'd get a shape that couldn't be cut out of a flat piece of paper. The smaller the pieces, the less you'll have to modify these values to get something flat.

 

[fauxtex]

I appreciate your help StatusX but I'm not following you. Suppose you have a paper dome. If you were to cut the dome so as to lay it flat, Say slicing it like the top half of an orange, into 8 sections, they would spread out and lay flat. The tops would come to a point then the sections would curve out. (If it were a sphere it would curve back in and come to a point again.) I'm trying to find the measurment of the arc of this 14' dome for the side measurments and the width of the bottom for each of these sections. I may have to cut it into more sections to get it to lay pretty flat but I'd rather not. I am painting a wrought iron looking structure with 8 sections. They will all look the same so I only need one template. This is much easier (I thought) than figuring it out on the ceiling.

 

[AlephZero]

I expect what you want is a template that is the same linear dimensions as your curved slice of dome. If you actually want to match it up with the curved dome you may need to slice up the template after you have made the design.

It's a fairly simple bit of geometry to work out the shape assuming the dome really is spherical as you described it. The picture is a section through the centre of the dome.

To find the radius of the dome r, use Pythagoras theorem

r^2 = (r-2)^2 + 7^2

r = 11.25 ft

To find max value of theta:

sin theta = 7/r, theta = 38.5 degrees

At any point P, the "height" of your template is the distance round the circle from the top of the dome
= r.theta (working in radians)
= 2 pi r theta / 360 (working in degrees)

The radius of the horizontal circle round the dome through P is r sin theta

So the "width" of the template at that point is 1/8 of the circumference of the circle = (2 pi r sin theta)/8

Work out the width and length from the top at say 10 different values of theta between 0 and 38.5 degrees and plot them out to make your template.

As a check, the angle between the two curved sides at the top of the template must be 360/8 = 45 degrees. At the bottom the width should by 1/8 of a 14 ft diameter circle = 14 pi /8

 

[fauxtex]

Thank you AlephaZero. This is what I was looking for! OOOO's

 

[KV-1]

A little late,

But this might help those struggling with the same problem.

Use a dymaxion map--simplify a sphere into a polyhedron:

http://en.wikipedia.org/wiki/Dymaxion_map

[URL]http://upload.wikimedia.org/wikipedia/commons/b/bb/Dymaxion_2003_animation_small1.gif[/URL]

and then transfer your design!